题目内容
一等腰三角形腰长6cm，一腰上的中线将其周长分成两部分，且两部分差为3cm，则底边长为多少？
考点：等腰三角形的性质
专题：
分析：先根据题意画出图形，设AE为底边上的高，由D为AC中点，得到AD=DC，再根据BD将其周长分成两部分的差为3cm，分别表示出BD分三角形周长的两部分，相减等于3列出关于BC的方程，求出方程的解得到BC的长．
解答：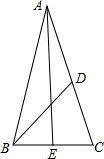
解：如图所示，AB=AC=6cm，D为AC中点，AE⊥BC于E．
∵D为AC的中点，
∴AD=DC=3cm，
根据题意得：（AB+AD）-（CB+CD）=3或（CB+CD）-（AB+AD）=3，
即（6+3）-（CB+3）=3或（CB+3）-（6+3）=3，
解得：BC=0cm或9cm，
故底边长为9cm．
解：如图所示，AB=AC=6cm，D为AC中点，AE⊥BC于E．∵D为AC的中点，
∴AD=DC=3cm，
根据题意得：（AB+AD）-（CB+CD）=3或（CB+CD）-（AB+AD）=3，
即（6+3）-（CB+3）=3或（CB+3）-（6+3）=3，
解得：BC=0cm或9cm，
故底边长为9cm．
点评：此题考查了等腰三角形的性质，以及勾股定理，要求学生借助图形，采用数形结合及分类讨论的思想，求出底边BC的长，同时注意因为没有指明周长分成两部分的长短，故BC求出有两解，不要遗漏．
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
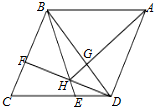如图，在菱形ABCD中，AB=BD=2，点E，F分别在边CD，BC上，且BF=CE．连接BE，DF相交于点H，连接AH，BD相交于点G．若BF：FC=2：1，则AH=
如图，在Rt△ABC中，∠C=90°，顶点A、C的坐标分别为（-1，2），（3，2），点B在x轴上，抛物线y=-x2+bx+c经过A、C两点．
如图所示的是一个棱长为3cm的正方体，假设一只蚂蚁每秒爬行2cm，则它从下底面A点沿表面爬行到右侧面的B点，最少要花几秒钟？（精确到0.1s）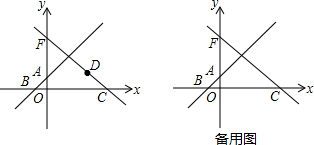
在平面直角坐标系xOy中，直线AB与直线y=-