题目内容
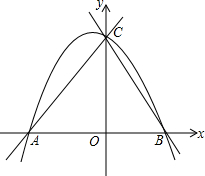 如图,二次函数y=ax2+2ax+4的图象与x轴交于点A、B,与y轴交于点C,OC:OB=2:1,
如图,二次函数y=ax2+2ax+4的图象与x轴交于点A、B,与y轴交于点C,OC:OB=2:1,(1)求此二次函数的解析式;
(2)动直线l从与直线AC重合的位置出发,绕点A顺时针旋转,与直线AB重合时终止运动,直线l与BC交于点D,P是线段AD的中点.
①直接写出点P所经过的路线长.
②点D与B、C不重合时,过点D作DE⊥AC于点E、作DF⊥AB于点F,连结PE、PF,在旋转过程中,∠EPF的大小是否发生变化?若不变,求∠EPF的度数;若变化,请说明理由.
③在②的条件下,连结EF,求EF的最小值.
考点:二次函数综合题
专题:
分析:(1)先令x=0求出OC的长度,再利用∠CBO正切值求出OB的长度,从而得到点B的坐标,然后代入二次函数解析式求出a的值,即可得解;
(2)①利用勾股定理列式求出BC,再判断出点P经过的路线为△ABC的中位线,然后根据三角形的中位线平行于第三边并且等于第三边的一半解答;
②根据直角三角形斜边上的中线等于斜边的一半可得EP=AP=
AD,FP=AP=
AD,再根据等边对等角可得∠CAD=∠AEP,∠BAD=∠AFP,然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠EPF=2∠BAC,令y=0,解关于x的一元二次方程求出点A的坐标,从而得到OA=OC,求出∠BAC=45°,即可得解;
③判断出△EFP是等腰直角三角形,从而确定AD⊥BC时,EF最短,利用△ABC的面积列式求出AD⊥BC时的值,再求出EP,然后根据等腰直角三角形的斜边等于直角边的
解答.
(2)①利用勾股定理列式求出BC,再判断出点P经过的路线为△ABC的中位线,然后根据三角形的中位线平行于第三边并且等于第三边的一半解答;
②根据直角三角形斜边上的中线等于斜边的一半可得EP=AP=
| 1 |
| 2 |
| 1 |
| 2 |
③判断出△EFP是等腰直角三角形,从而确定AD⊥BC时,EF最短,利用△ABC的面积列式求出AD⊥BC时的值,再求出EP,然后根据等腰直角三角形的斜边等于直角边的
| 2 |
解答:解:(1)令x=0,则y=4,
∴OC=4,
∵OC:OB=2:1,
∴
=
=2,
解得OB=2,
∴点B的坐标为(2,0),
代入二次函数y=ax2+2ax+4得,4a+2a•2+4=0,
解得a=-
,
∴二次函数解析式为y=-
x2-x+4;
(2)①在Rt△OBC中,BC=
=
=2
,
∵P是线段AD的中点,
∴点P经过的路线为△ABC的中位线,
长度为:
BC=
×2
=
;
②∵DE⊥AC,DF⊥AB,P是线段AD的中点,
∴EP=AP=
AD,FP=AP=
AD,
∴∠CAD=∠AEP,∠BAD=∠AFP,
∴∠EPF=∠EPD+∠FPD=∠CAD+∠AEP+∠BAD+∠AFP=2∠CAD+2∠BAD=2∠BAC,
令y=0,则-
x2-x+4=0,
整理得,x2+2x-8=0,
解得x1=2,x2=-4,
∴点A坐标为(-4,0),
∴OA=OC=4,
∴∠BAC=45°,
∴∠EPF=2×45°=90°;
③∵EP=AP=
AD,FP=AP=
AD,
∴EP=FP,
∵∠EPF=90°,
∴△EFP是等腰直角三角形,
∴AD⊥BC时,EF最短,
此时,S△ABC=
AB•OC=
BC•AD,
即
×|-4-2|×4=
×2
AD,
解得AD=
,
∴EP=
AD=
,
∴EF最小=
EP=
×
=
.
∴OC=4,
∵OC:OB=2:1,
∴
| OC |
| OB |
| 4 |
| OB |
解得OB=2,
∴点B的坐标为(2,0),
代入二次函数y=ax2+2ax+4得,4a+2a•2+4=0,
解得a=-
| 1 |
| 2 |
∴二次函数解析式为y=-
| 1 |
| 2 |
(2)①在Rt△OBC中,BC=
| OC2+OB2 |
| 42+22 |
| 5 |
∵P是线段AD的中点,
∴点P经过的路线为△ABC的中位线,
长度为:
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
②∵DE⊥AC,DF⊥AB,P是线段AD的中点,
∴EP=AP=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CAD=∠AEP,∠BAD=∠AFP,
∴∠EPF=∠EPD+∠FPD=∠CAD+∠AEP+∠BAD+∠AFP=2∠CAD+2∠BAD=2∠BAC,
令y=0,则-
| 1 |
| 2 |

整理得,x2+2x-8=0,
解得x1=2,x2=-4,
∴点A坐标为(-4,0),
∴OA=OC=4,
∴∠BAC=45°,
∴∠EPF=2×45°=90°;
③∵EP=AP=
| 1 |
| 2 |
| 1 |
| 2 |
∴EP=FP,
∵∠EPF=90°,
∴△EFP是等腰直角三角形,
∴AD⊥BC时,EF最短,
此时,S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
解得AD=
12
| ||
| 5 |
∴EP=
| 1 |
| 2 |
6
| ||
| 5 |
∴EF最小=
| 2 |
| 2 |
6
| ||
| 5 |
6
| ||
| 5 |
点评:本题是二次函数综合题型,主要考查了待定系数法求函数解析式,锐角三角函数,三角形的中位线定理,直角三角形斜边上的中线等于斜边的一半的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,等腰直角三角形的判定与性质,三角形的面积的应用,综合性较强,难度较大,熟记各性质是解题的关键.

练习册系列答案
相关题目
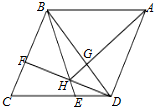 如图,在菱形ABCD中,AB=BD=2,点E,F分别在边CD,BC上,且BF=CE.连接BE,DF相交于点H,连接AH,BD相交于点G.若BF:FC=2:1,则AH=
如图,在菱形ABCD中,AB=BD=2,点E,F分别在边CD,BC上,且BF=CE.连接BE,DF相交于点H,连接AH,BD相交于点G.若BF:FC=2:1,则AH= 有理数a,b在数轴上的对应的位置如图所示:
有理数a,b在数轴上的对应的位置如图所示: 如图,已知?ABCD中,点E为BC延长线上的点,若S?ABCD=20cm2,S△CEF=9cm2,则S△ADF=
如图,已知?ABCD中,点E为BC延长线上的点,若S?ABCD=20cm2,S△CEF=9cm2,则S△ADF= 如图,在Rt△ABC中,∠C=90°,顶点A、C的坐标分别为(-1,2),(3,2),点B在x轴上,抛物线y=-x2+bx+c经过A、C两点.
如图,在Rt△ABC中,∠C=90°,顶点A、C的坐标分别为(-1,2),(3,2),点B在x轴上,抛物线y=-x2+bx+c经过A、C两点.