题目内容
如图1,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C(0,2),点P是抛物线上的一个动点,过点P作PQ⊥x轴,垂足为Q,交直线BC于点D.
(1)求该抛物线的函数表达式;
(2)若以P、D、O、C为顶点的四边形是平行四边形,求点Q的坐标;
(3)如图2,当点P位于直线BC上方的抛物线上时,过点P作PE⊥BC于点E,设△PDE的面积为S,求当S取得最大值时点P的坐标,并求S的最大值.
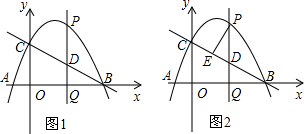
(1)求该抛物线的函数表达式;
(2)若以P、D、O、C为顶点的四边形是平行四边形,求点Q的坐标;
(3)如图2,当点P位于直线BC上方的抛物线上时,过点P作PE⊥BC于点E,设△PDE的面积为S,求当S取得最大值时点P的坐标,并求S的最大值.

考点:二次函数综合题
专题:
分析:(1)把A、B、C三点的坐标代入可求得a、b、c的值,可得出函数表达式;
(2)可先求得BC的解析式,设出Q点坐标,可表示出D点坐标和P点坐标,可表示出PD的长,由条件可得PD=OC=2,可求得P点坐标,则可得Q点的坐标;
(3)可设出P的坐标,由PQ∥OC可表示出DQ、BD,由△PED∽△BQD可表示出PE和DE,则可表示出S,再结合P在直线BC上方,可求得S的最大值,可求得P点的坐标.
(2)可先求得BC的解析式,设出Q点坐标,可表示出D点坐标和P点坐标,可表示出PD的长,由条件可得PD=OC=2,可求得P点坐标,则可得Q点的坐标;
(3)可设出P的坐标,由PQ∥OC可表示出DQ、BD,由△PED∽△BQD可表示出PE和DE,则可表示出S,再结合P在直线BC上方,可求得S的最大值,可求得P点的坐标.
解答:解:(1)∵二次函数与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C(0,2),
∴代入二次函数解析式可得
,
解得
,
∴二次函数表达式为y=-
x2+
x+2;
(2)设直线BC解析式为y=kx+b,
∵B(4,0),C(0,2),
∴代入可得
,
解得
,
∴直线BC解析式为y=-
x+2,
设Q坐标为(m,0),则可知D点坐标为(m,-
m+2),
又∵P点在抛物线上,
∴P点坐标为(m,-
m2+
m+2),
当P、D、O、C为顶点的四边形为平行四边形时,则有PD=OC=2,
即|-
m2+
m+2-(-
m+2)|=2,即|-
m2+2m|=2,
当-
m2+2m=2时,解得m=2,则Q坐标为(2,0),
当-
m2+2m=-2时,解得m=2±2
,则Q坐标为(2+
,0)或(2-
,0),
综上可知Q点坐标为(2,0)或(2+2
,0)或(2-2
,0);
(3)设Q点坐标为(n,0),由(2)可知D为(n,-
n+2),P点坐标为(n,-
n2+
n+2),
∴PD=-
n2+2n=
n(4-n),DQ=-
n+2,
又∵OB=4,
∴BQ=4-n,
在Rt△OBC中,OC=2,OB=4,由勾股定理可求得BC=2
,
∵OQ∥OC,
∴
=
,即
=
,解得BD=
,
∵PE⊥BC,PQ⊥QB,
∴∠PED=∠BQD=90°,且∠PDE=∠BDQ,
∴△PED∽△BQD,
∴
=
=
=
=
,
即
=
=
,
解得PE=
,DE=
n(4-n),
∴S=
PE•DE=
×
×
=
(-n2+4n)2,
令t=-n2+4n=-(n-2)2+4,
∵P在直线BC上方,
∴0<n<4,
∴0<t≤4,且当n=2时,t有最大值4,
此时P点坐标为(2,3),
∴当t=4时,Smax=
×42=
,
综上可知当P为(2,3)时,S有最大值,最大值为=
.
∴代入二次函数解析式可得
|
解得
|
∴二次函数表达式为y=-
| 1 |
| 2 |
| 3 |
| 2 |
(2)设直线BC解析式为y=kx+b,
∵B(4,0),C(0,2),
∴代入可得
|
解得
|
∴直线BC解析式为y=-
| 1 |
| 2 |
设Q坐标为(m,0),则可知D点坐标为(m,-
| 1 |
| 2 |
又∵P点在抛物线上,
∴P点坐标为(m,-
| 1 |
| 2 |
| 3 |
| 2 |
当P、D、O、C为顶点的四边形为平行四边形时,则有PD=OC=2,
即|-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当-
| 1 |
| 2 |
当-
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
综上可知Q点坐标为(2,0)或(2+2
| 2 |
| 2 |
(3)设Q点坐标为(n,0),由(2)可知D为(n,-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴PD=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵OB=4,
∴BQ=4-n,
在Rt△OBC中,OC=2,OB=4,由勾股定理可求得BC=2
| 5 |
∵OQ∥OC,
∴
| BD |
| BC |
| BQ |
| OB |
| BD | ||
2
|
| 4-n |
| 4 |
| ||
| 2 |
∵PE⊥BC,PQ⊥QB,
∴∠PED=∠BQD=90°,且∠PDE=∠BDQ,
∴△PED∽△BQD,
∴
| PE |
| BQ |
| DE |
| DQ |
| PD |
| BD |
| ||||
|
| n | ||
|
即
| PE |
| 4-n |
| DE | ||
-
|
| n | ||
|
解得PE=
| n(4-n) | ||
|
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| n(4-n) | ||
|
| n(4-n) |
| 2 |
| ||
| 20 |
令t=-n2+4n=-(n-2)2+4,
∵P在直线BC上方,
∴0<n<4,
∴0<t≤4,且当n=2时,t有最大值4,
此时P点坐标为(2,3),
∴当t=4时,Smax=
| ||
| 20 |
4
| ||
| 5 |
综上可知当P为(2,3)时,S有最大值,最大值为=
4
| ||
| 5 |
点评:本题主要考查待定系数法求函数解析式及平行四边形的性质、平行线分线段成比例和相似三角形的判定和性质.在(1)中注意待定系数法应用的关键是点的坐标,在(2)中用Q的坐标表示出PD的长度,得到关于Q点坐标的方程是解题的关键,在(3)中用Q点的坐标表示出PE、DE的长度是解题的关键.本题知识点多,计算量大,难度较大.

练习册系列答案
相关题目
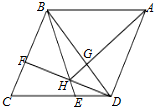 如图,在菱形ABCD中,AB=BD=2,点E,F分别在边CD,BC上,且BF=CE.连接BE,DF相交于点H,连接AH,BD相交于点G.若BF:FC=2:1,则AH=
如图,在菱形ABCD中,AB=BD=2,点E,F分别在边CD,BC上,且BF=CE.连接BE,DF相交于点H,连接AH,BD相交于点G.若BF:FC=2:1,则AH= 如图,已知?ABCD中,点E为BC延长线上的点,若S?ABCD=20cm2,S△CEF=9cm2,则S△ADF=
如图,已知?ABCD中,点E为BC延长线上的点,若S?ABCD=20cm2,S△CEF=9cm2,则S△ADF=
 如图,在Rt△ABC中,∠C=90°,顶点A、C的坐标分别为(-1,2),(3,2),点B在x轴上,抛物线y=-x2+bx+c经过A、C两点.
如图,在Rt△ABC中,∠C=90°,顶点A、C的坐标分别为(-1,2),(3,2),点B在x轴上,抛物线y=-x2+bx+c经过A、C两点. 如图所示的是一个棱长为3cm的正方体,假设一只蚂蚁每秒爬行2cm,则它从下底面A点沿表面爬行到右侧面的B点,最少要花几秒钟?(精确到0.1s)
如图所示的是一个棱长为3cm的正方体,假设一只蚂蚁每秒爬行2cm,则它从下底面A点沿表面爬行到右侧面的B点,最少要花几秒钟?(精确到0.1s)