题目内容
11.某商场将进货价为每只30元的台灯以每只40元售出,平均每月能售出600只.调查表明,这种台灯的售价每上涨1元,其销售量将减少10只.当这种台灯的售价定为多少元时,每个月的利润恰为10 000元?分析 设这种台灯的售价为x元,根据一台的利润×总的台数=总的利润和这种台灯的售价每上涨1元,其销售量将减少10只,列出方程,再求解即可.
解答 解:设这种台灯的售价为x元,根据题意得:
[600-10(x-40)](x-30)=10000,
解得x1=50,x2=80,
答:当这种台灯的售价定为50或80元时,每个月的利润恰为10000元.
点评 此题考查了一元二次方程的应用,解题关键是根据题目给出的条件,找出合适的等量关系,列出方程;难度一般,是常考题.

练习册系列答案
相关题目
12.下列各数中最小的是( )
| A. | -5 | B. | -π | C. | 3 | D. | 0 |
13.在函数y=$\frac{\sqrt{x+4}}{x}$中,自变量x的取值范围是( )
| A. | x>0 | B. | x≥-4 | C. | x≥-4且x≠0 | D. | x>0且x≠-1 |
6.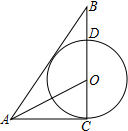 如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( )
如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( )
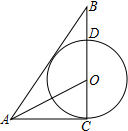 如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( )
如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( )| A. | π | B. | 2π | C. | $\frac{9}{4}π$ | D. | $\frac{16}{9}π$ |
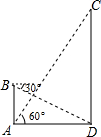 如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米.
如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米. 如图,在⊙O的内接五边形ABCDE中,∠CAD=40°,则∠B+∠E=220°.
如图,在⊙O的内接五边形ABCDE中,∠CAD=40°,则∠B+∠E=220°.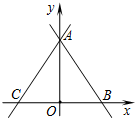 如图,直线AB的函数关系式为y=-$\frac{3}{2}$x+3,直线AC与直线AB关于y轴成轴对称,则直线AC的函数关系式为y=$\frac{3}{2}$x+3.
如图,直线AB的函数关系式为y=-$\frac{3}{2}$x+3,直线AC与直线AB关于y轴成轴对称,则直线AC的函数关系式为y=$\frac{3}{2}$x+3.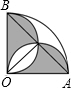 如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为$\frac{1}{2}$cm2.
如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为$\frac{1}{2}$cm2.