题目内容
6.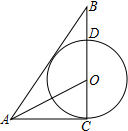 如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( )
如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( )| A. | π | B. | 2π | C. | $\frac{9}{4}π$ | D. | $\frac{16}{9}π$ |
分析 作OE⊥AB于E,如图,设⊙O的半径为r,根据切线的性质得OE=r,再在△AOC中利用正切定义得到AC=2r,在Rt△OBE中利用勾股定理得到BE=$\sqrt{2r+1}$,然后证明RtBEO∽Rt△BCA,则利用相似比得到$\frac{r}{2r}$=$\frac{\sqrt{2r+1}}{2r+1}$,再解方程求出r后计算⊙O的面积.
解答 解:作OE⊥AB于E,如图, 设⊙O的半径为r,
设⊙O的半径为r,
∵AB为切线,
∴OE=r,
在△AOC中,∠ACO=90°,
∵tan∠AOC=$\frac{AC}{OC}$=2,
∴AC=2r,
在Rt△OBE中,BE=$\sqrt{O{B}^{2}-O{E}^{2}}$=$\sqrt{(r+1)^{2}-{r}^{2}}$=$\sqrt{2r+1}$,
∵∠EBO=∠CBA,
∴RtBEO∽Rt△BCA,
∴$\frac{OE}{AC}$=$\frac{BE}{BC}$,即$\frac{r}{2r}$=$\frac{\sqrt{2r+1}}{2r+1}$,解得r=$\frac{3}{2}$,
∴⊙O的面积=π•($\frac{3}{2}$)2=$\frac{9}{4}$π.
故选C.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径;若出现圆的切线,则作垂线得到半径.解决本题的关键是用半径表示AC、BE,然后利用相似比得到关于半径的方程.

练习册系列答案
相关题目
8.为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的同学捐书册数分别是:5,7,x,3,4,6.已知他们平均每人捐5本,则这组数据的众数、中位数和方差分别是( )
| A. | 5,5,$\frac{3}{2}$ | B. | 5,5,10 | C. | 6,5.5,$\frac{11}{6}$ | D. | 5,5,$\frac{5}{3}$ |
11.某商场将进货价为每只30元的台灯以每只40元售出,平均每月能售出600只.调查表明,这种台灯的售价每上涨1元,其销售量将减少10只.当这种台灯的售价定为多少元时,每个月的利润恰为10 000元?
16. 某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )
某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )
 某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )
某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )| A. | $\frac{31}{2}$,15 | B. | 15,$\frac{31}{2}$ | C. | 15,15 | D. | $\frac{31}{2}$,$\frac{31}{2}$ |
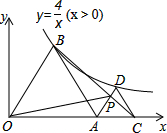 如图,△AOB与△ACD均为正三角形,且顶点B、D均在双曲线y=$\frac{4}{x}$(x>0)上,点A、C在x轴上,连接BC交AD于点P,则△OBP的面积=4.
如图,△AOB与△ACD均为正三角形,且顶点B、D均在双曲线y=$\frac{4}{x}$(x>0)上,点A、C在x轴上,连接BC交AD于点P,则△OBP的面积=4. 如图,⊙O为△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,D为⊙O上一点,∠ABC=∠ODC=67.5°.
如图,⊙O为△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,D为⊙O上一点,∠ABC=∠ODC=67.5°.