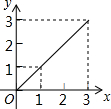题目内容
16. 如图,在⊙O的内接五边形ABCDE中,∠CAD=40°,则∠B+∠E=220°.
如图,在⊙O的内接五边形ABCDE中,∠CAD=40°,则∠B+∠E=220°.
分析 连接CE,根据圆内接四边形对角互补可得∠B+∠AEC=180°,再根据同弧所对的圆周角相等可得∠CED=∠CAD,然后求解即可.
解答  解:如图,连接CE,
解:如图,连接CE,
∵五边形ABCDE是圆内接五边形,
∴四边形ABCE是圆内接四边形,
∴∠B+∠AEC=180°,
∵∠CED=∠CAD=40°,
∴∠B+∠E=180°+40°=220°.
故答案为:220.
点评 本题考查了圆周角定理及圆内接四边形的性质,同弧所对的圆周角相等的性质,熟记性质并作辅助线构造出圆内接四边形是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
17.已知下列命题:
①同位角相等;
②若a>b>0,则$\frac{1}{a}<\frac{1}{b}$;
③对角线相等且互相垂直的四边形是正方形;
④抛物线y=x2-2x与坐标轴有3个不同交点;
⑤边长相等的多边形内角都相等.
其中正确的命题有( )
①同位角相等;
②若a>b>0,则$\frac{1}{a}<\frac{1}{b}$;
③对角线相等且互相垂直的四边形是正方形;
④抛物线y=x2-2x与坐标轴有3个不同交点;
⑤边长相等的多边形内角都相等.
其中正确的命题有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4. 由圆柱体和长方体组成的几何体如图所示,其俯视图是( )
由圆柱体和长方体组成的几何体如图所示,其俯视图是( )
 由圆柱体和长方体组成的几何体如图所示,其俯视图是( )
由圆柱体和长方体组成的几何体如图所示,其俯视图是( )| A. |  | B. |  | C. |  | D. |  |
11.某商场将进货价为每只30元的台灯以每只40元售出,平均每月能售出600只.调查表明,这种台灯的售价每上涨1元,其销售量将减少10只.当这种台灯的售价定为多少元时,每个月的利润恰为10 000元?
8.大学生自主创业,集资5万元开品牌专卖店,已知该品牌商品成本为每件a元,市场调查发现日销售量y(件)与销售价x(元/件)之间存在一次函数关系如表:
若该店某天的销售价定为110元/件,雇有3名员工,则当天正好收支平衡(其中支出=商品成本+员工工资+应支付其它费用):已知员工的工资为每人每天100元,每天还应支付其它费用为200元(不包括集资款).
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)该店现有2名员工,试求每件服装的销售价定为多少元时,该服装店每天的毛利润最大:(毛利润═销售收入一商品成本一员工工资一应支付其他费用)
(3)在(2)的条件下,若每天毛利润全部积累用于一次性还款,而集资款每天应按其万分之二的利率支付利息,则该店最少需要多少天(取整数)才能还清集资款?
| 销售价x(元/件) | … | 110 | 115 | 120 | 125 | 130 | … |
| 销售量y(件) | … | 50 | 45 | 40 | 35 | 30 | … |
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)该店现有2名员工,试求每件服装的销售价定为多少元时,该服装店每天的毛利润最大:(毛利润═销售收入一商品成本一员工工资一应支付其他费用)
(3)在(2)的条件下,若每天毛利润全部积累用于一次性还款,而集资款每天应按其万分之二的利率支付利息,则该店最少需要多少天(取整数)才能还清集资款?
5.下列计算正确的是( )
| A. | a+a=2a | B. | b3•b3=2b3 | C. | a3+a=3 | D. | (a5)2=a7 |
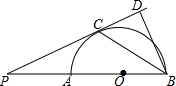 如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
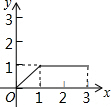
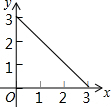
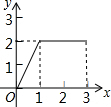
 如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积y与点P运动的路程x之间的函数图象大致是( )
如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积y与点P运动的路程x之间的函数图象大致是( )