题目内容
7.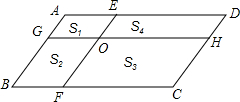 如图,在平行四边形ABCD中,AB∥EF,AD∥GH,EF与GH交于点O,分别的4个小平行四边形的面积分别为S1,S2,S3,S4,若S1=8,S2=10,S3=30,则S4=24.
如图,在平行四边形ABCD中,AB∥EF,AD∥GH,EF与GH交于点O,分别的4个小平行四边形的面积分别为S1,S2,S3,S4,若S1=8,S2=10,S3=30,则S4=24.
分析 先证明$\frac{{S}_{1}}{{S}_{2}}$=$\frac{{S}_{4}}{{S}_{3}}$,然后代入计算即可.
解答 解: ∵四边形ABCD是平行四边形,AB∥EF,AD∥GH,
∵四边形ABCD是平行四边形,AB∥EF,AD∥GH,
∴AB∥EF∥CD,AD∥GH∥BC,
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{EO}{OF}$,$\frac{{S}_{4}}{{S}_{3}}$=$\frac{EO}{OF}$,
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{{S}_{4}}{{S}_{3}}$,
∴$\frac{8}{10}$=$\frac{{S}_{4}}{30}$,
S4=24.
点评 本题考查平行四边形的性质、解题的关键是通过求出S1与S2,S4与S3的面积比,发现S1,S2,S3,S4之间关系,记住这个关系式,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.校办工厂要制作一些等腰三角形模具,工人师傅对四个模具的尺寸按照底边、腰长和底边上的高的顺序进行了记录,其中记录错误的是( )
| A. | 10,26,24 | B. | 16,10,6 | C. | 30,17,8 | D. | 24,13,5 |
8. 如图,点C在以AB为直径的半圆上,AB=2,∠CBA=30°,点D到线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是( )
如图,点C在以AB为直径的半圆上,AB=2,∠CBA=30°,点D到线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是( )
 如图,点C在以AB为直径的半圆上,AB=2,∠CBA=30°,点D到线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是( )
如图,点C在以AB为直径的半圆上,AB=2,∠CBA=30°,点D到线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
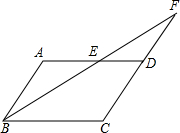 如图,在?ABCD中,AB=4,AD=7,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF的长是( )
如图,在?ABCD中,AB=4,AD=7,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF的长是( )
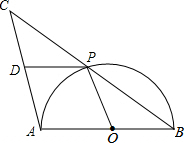 如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.
如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.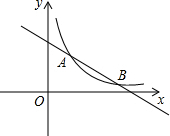 如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数的图象相交于点A、B,点A的坐标为(2,3),点B的横坐标为6.
如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数的图象相交于点A、B,点A的坐标为(2,3),点B的横坐标为6.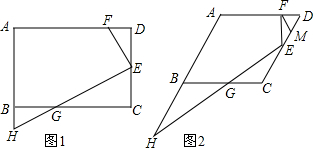
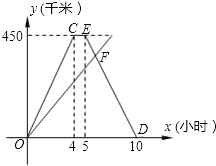 A、B两地间的公路长为450千米,甲、乙两车同时从A地出发沿这一公路驶向B地,甲车到达1小时后沿原路返回,如图是它们离A地的距离y(千米)与行驶时间x(小时)之间的函数图象.
A、B两地间的公路长为450千米,甲、乙两车同时从A地出发沿这一公路驶向B地,甲车到达1小时后沿原路返回,如图是它们离A地的距离y(千米)与行驶时间x(小时)之间的函数图象.