题目内容
15.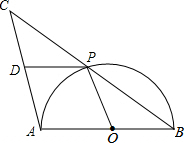 如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.
如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.(1)求证:△CDP≌△POB;
(2)连接OD,当四边形BPDO是菱形时,求∠PBA的度数.
分析 (1)根据三角形中位线定理可得DP∥DB,DP=$\frac{1}{2}$AB,进而可得∠CPD=∠PBO,然后再证明BO=DP,可利用SAS判定:△CDP≌△POB;
(2)连接OD,根据全等可得DP=OB,再由AO=BO可得DP=AO=OB,再由DP∥OB可得四边形BPDO是平行四边形,然后再利用菱形的性质可得OB=BP,从而证明△PBO是等边三角形,进而可得答案.
解答 解:(1)∵点D是AC的中点,PC=PB,
∴DP∥DB,DP=$\frac{1}{2}$AB,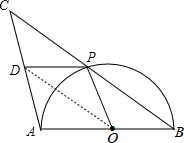
∴∠CPD=∠PBO.
∵BO=$\frac{1}{2}$AB,
∴DP=OB,
在△CDP和△POB中$\left\{\begin{array}{l}{CP=PB}\\{∠PBO=∠CPD}\\{PD=OB}\end{array}\right.$,
∴△CDP≌△POB(SAS);
(2)连接OD,
∵由(1)得DP=AO=OB,DP∥OB,
∴四边形BPDO是平行四边形,
∴当OB=BP时,四边形BPDO是菱形,
∵PO=BO,
∴△PBO是等边三角形,
∴∠PBA=60°.
点评 此题主要考查了菱形的性质,以及全等三角形的判定和性质,关键是掌握菱形邻边相等,三角形的中位线平行于第三边,且等于第三边的一半.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
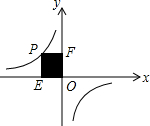 如图,点P是反比例函数在第二象限上的一点,且矩形PEOF的面积为5,则反比例函数的表达式为y=-$\frac{5}{x}$.
如图,点P是反比例函数在第二象限上的一点,且矩形PEOF的面积为5,则反比例函数的表达式为y=-$\frac{5}{x}$.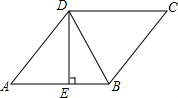 如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{4}{5}$,BE=2,则tan∠DBE=3.
如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{4}{5}$,BE=2,则tan∠DBE=3. 如图,在矩形ABCD中,BC=2,M为对角线BD的中点,连接CM,以CM为直径作⊙O交BD于点E,连接AE,当直线AE与⊙O相切时,AB的长为$\sqrt{6}$-$\sqrt{2}$.
如图,在矩形ABCD中,BC=2,M为对角线BD的中点,连接CM,以CM为直径作⊙O交BD于点E,连接AE,当直线AE与⊙O相切时,AB的长为$\sqrt{6}$-$\sqrt{2}$.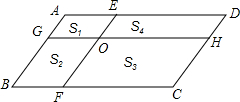 如图,在平行四边形ABCD中,AB∥EF,AD∥GH,EF与GH交于点O,分别的4个小平行四边形的面积分别为S1,S2,S3,S4,若S1=8,S2=10,S3=30,则S4=24.
如图,在平行四边形ABCD中,AB∥EF,AD∥GH,EF与GH交于点O,分别的4个小平行四边形的面积分别为S1,S2,S3,S4,若S1=8,S2=10,S3=30,则S4=24.