题目内容
10.不等式组$\left\{\begin{array}{l}5≥x-3(x-1)\\ \frac{x+2}{2}>x\end{array}\right.$的解集用数轴表示正确的是( )| A. |  | B. |  | C. |  | D. |  |
分析 首先解每个不等式,然后把每个解集在数轴上表示出来.
解答 解:$\left\{\begin{array}{l}{5≥x-3(x-1)…①}\\{\frac{x+2}{2}>x…②}\end{array}\right.$,
解①得:x≥-1,
解②得:x<2.
则表示为: .
.
故选B.
点评 本题考查了不等式组的解法,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
20.某不等式的解集x≤-1在数轴上的表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
1.已知,不等式组$\left\{\begin{array}{l}{x>a}\\{-x+5>0}\end{array}\right.$只有3个整数解,则a的取值范围是( )
| A. | 1<x<2 | B. | 1≤x<2 | C. | 1<x≤2 | D. | 1≤x≤2 |
18.已知点P(a,b)是反比例函数$y=\frac{4}{x}$图象上异于点(-2,-2)的一个动点,则$\frac{1}{2+a}+\frac{1}{2+b}$的值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 4 |
5.已知∠A的两边与∠B的两边互相平行,且∠A=20°,则∠B的度数为( )
| A. | 20° | B. | 80° | C. | 160° | D. | 20°或160° |
2.下列命题中真命题的是( )
| A. | 如果a=b,b=c,那么a=c | B. | 如果a<0,b<0,那么ab<0 | ||
| C. | 内错角相等 | D. | 一个角的补角大于这个角 |
19.顺次连接一个矩形各边的中点,得到的四边形一定是( )
| A. | 菱形 | B. | 矩形 | C. | 正方形 | D. | 梯形 |
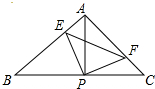 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③△PEF是等腰直角三角形,④S四边形AEPF=$\frac{1}{2}$S△ABC,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确有 ( )
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③△PEF是等腰直角三角形,④S四边形AEPF=$\frac{1}{2}$S△ABC,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确有 ( )