题目内容
19．顺次连接一个矩形各边的中点，得到的四边形一定是（ ）| A． | 菱形 | B． | 矩形 | C． | 正方形 | D． | 梯形 |
分析 三角形的中位线平行于第三边，且等于第三边的一半．需注意新四边形的形状只与对角线有关，不用考虑原四边形的形状．
解答 
解：如图，连接AC、BD．
在△ABD中，
∵AH=HD，AE=EB，
∴EH=$\frac{1}{2}$BD，
同理FG=$\frac{1}{2}$BD，HG=$\frac{1}{2}$AC，EF=$\frac{1}{2}$AC，
又∵在矩形ABCD中，AC=BD，
∴EH=HG=GF=FE，
∴四边形EFGH为菱形．
故选A．
点评 本题考查了菱形的判定，菱形的判别方法是说明一个四边形为菱形的理论依据，常用三种方法：①定义，②四边相等，③对角线互相垂直平分．
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
9．下列式子中，为最简二次根式的是（ ）
| A． | $\sqrt{10}$ | B． | $\sqrt{8}$ | C． | $\sqrt{\frac{1}{2}}$ | D． | $\frac{1}{{\sqrt{2}}}$ |
10．不等式组$\left\{\begin{array}{l}5≥x-3（x-1）\\ \frac{x+2}{2}＞x\end{array}\right.$的解集用数轴表示正确的是（ ）
| A． |  | B． |  | C． |  | D． |  |
7．方程组$\left\{\begin{array}{l}{x-1=0}\\{x+1=y}\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$ |
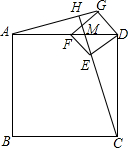如图，若四边形ABCD、四边形GFED都是正方形，AD=4，$DE=\sqrt{2}$，当正方形GFED绕D旋转到如图的位置，点F在边AD上，延长CE交AG于H，交AD于M．则CM的长为$\frac{4}{3}\sqrt{10}$．
如图，数轴上表示的是关于x的不等式组中两个不等式的解集，则这个不等式组的解集为2≤x≤3．