题目内容
18.已知点P(a,b)是反比例函数$y=\frac{4}{x}$图象上异于点(-2,-2)的一个动点,则$\frac{1}{2+a}+\frac{1}{2+b}$的值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 4 |
分析 由点P是反比例函数图象上异于点(-2,-2)的一点即可得出ab=4,且a≠-2,b≠-2,将分式$\frac{1}{2+a}+\frac{1}{2+b}$通分后代入ab的值即可得出结论.
解答 解:∵点P(a,b)是反比例函数$y=\frac{4}{x}$图象上异于点(-2,-2)的一个动点,
∴ab=4,且a≠-2,b≠-2.
∵$\frac{1}{2+a}+\frac{1}{2+b}$=$\frac{2+b+2+a}{(2+a)(2+b)}$=$\frac{4+a+b}{4+2(a+b)+ab}$=$\frac{4+a+b}{8+2(a+b)}$=$\frac{1}{2}$.
故选A.
点评 本题考查了反比例函数图象上点的坐标特征,解题的关键是求出$\frac{1}{2+a}+\frac{1}{2+b}$=$\frac{1}{2}$.本题属于基础题,难度不大,解决该题型题目时,根据点在反比例函数图象上,利用反比例函数图象上点的坐标特征找出该点横纵坐标之间的关系是关键.

练习册系列答案
相关题目
8.将函数y=-3x+1沿y轴向上平移4个单位长度后,所得图象对应的函数关系式为( )
| A. | y=-3(x+4)+1 | B. | y=-(x-4)+1 | C. | y=-3x+5 | D. | y=-3x-3 |
9.下列式子中,为最简二次根式的是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{8}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\frac{1}{{\sqrt{2}}}$ |
6.一个寻宝游戏的寻宝通道由正方形ABCD的边组成,如图1所示.为记录寻宝者的行进路线,在AB的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图2所示,则寻宝者的行进路线可能为( )
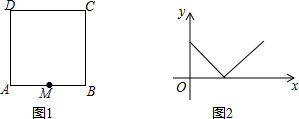
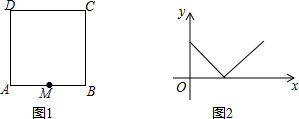
| A. | A→B | B. | B→C | C. | C→D | D. | D→A |
13.小颖随机抽样调查本班20名女同学所穿运动鞋尺码,并统计如表:
学校附近的商店经理根据表中决定本月多进尺码为23.0cm的女式运动鞋,商店经理的这一决定应用了哪个统计知识( )
| 尺码/cm | 21.5 | 22.0 | 22.5 | 23.0 | 23.5 |
| 人数 | 2 | 4 | 3 | 8 | 3 |
| A. | 众数 | B. | 中位数 | C. | 平均数 | D. | 方差 |
3. 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=10,则FD的长为( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=10,则FD的长为( )
 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=10,则FD的长为( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=10,则FD的长为( )| A. | $\frac{25}{3}$ | B. | 4 | C. | $\frac{25}{6}$ | D. | 5 |
10.不等式组$\left\{\begin{array}{l}5≥x-3(x-1)\\ \frac{x+2}{2}>x\end{array}\right.$的解集用数轴表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
7.方程组$\left\{\begin{array}{l}{x-1=0}\\{x+1=y}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$ |
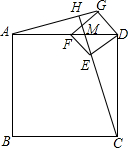 如图,若四边形ABCD、四边形GFED都是正方形,AD=4,$DE=\sqrt{2}$,当正方形GFED绕D旋转到如图的位置,点F在边AD上,延长CE交AG于H,交AD于M.则CM的长为$\frac{4}{3}\sqrt{10}$.
如图,若四边形ABCD、四边形GFED都是正方形,AD=4,$DE=\sqrt{2}$,当正方形GFED绕D旋转到如图的位置,点F在边AD上,延长CE交AG于H,交AD于M.则CM的长为$\frac{4}{3}\sqrt{10}$.