题目内容
15.分式方程$\frac{x}{x-1}$-1=$\frac{m}{(x-1)(x+1)}$有增根,则m的值为2或0.分析 分式方程去分母转化为整式方程,由分式方程有增根,得到(x+1)(x-1)=0,求出x的值,代入整式方程求出m的值即可.
解答 解:分式方程去分母得:x2+x-x2+1=m,即x+1=m,
由分式方程有增根,得到(x+1)(x-1)=0,
解得:x=1或x=-1,
把x=1代入整式方程得:m=2;
把x=-1代入整式方程得:m=0,
则m的值是2或0.
故答案为:2或0
点评 此题考查了分式方程的增根,增根确定后可按如下步骤进行:①化分式方程为整式方程;②把增根代入整式方程即可求得相关字母的值.

练习册系列答案
相关题目
5.为庆祝“六一”儿童节,某班学生准备分组外出活动,若每组8人,则余下2人;若每组9人,则少5人,求该班人数x和应分成的组数y,依题意得方程组为( )
| A. | $\left\{\begin{array}{l}{8y=x+2}\\{9y+5=x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{8y+2=x}\\{9y=x-5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{8y=x-2}\\{9y=x+5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{8y=x+2}\\{9y=x+5}\end{array}\right.$ |
6.一个寻宝游戏的寻宝通道由正方形ABCD的边组成,如图1所示.为记录寻宝者的行进路线,在AB的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图2所示,则寻宝者的行进路线可能为( )
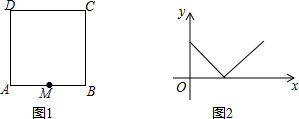
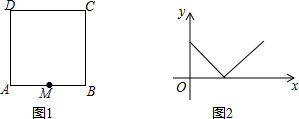
| A. | A→B | B. | B→C | C. | C→D | D. | D→A |
3. 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=10,则FD的长为( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=10,则FD的长为( )
 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=10,则FD的长为( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=10,则FD的长为( )| A. | $\frac{25}{3}$ | B. | 4 | C. | $\frac{25}{6}$ | D. | 5 |
10.不等式组$\left\{\begin{array}{l}5≥x-3(x-1)\\ \frac{x+2}{2}>x\end{array}\right.$的解集用数轴表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
20.某种计算机完成一次基本运算的时间约为0.000000003秒,把数据0.000000003用科学记数法表示为( )
| A. | 0.3×10-8 | B. | 0.3×10-9 | C. | 3×10-8 | D. | 3×10-9 |
7.方程组$\left\{\begin{array}{l}{x-1=0}\\{x+1=y}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$ |
 如图,∠2的同旁内角是∠4.
如图,∠2的同旁内角是∠4.