题目内容
4.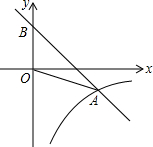 如图,平面直角坐标系中,点A是反比例函数y1=$\frac{k}{x}$(x>0)的图象上一点,一次函数y2=-x+2的图象经过点A,交y轴于点B,△AOB的面积是3.
如图,平面直角坐标系中,点A是反比例函数y1=$\frac{k}{x}$(x>0)的图象上一点,一次函数y2=-x+2的图象经过点A,交y轴于点B,△AOB的面积是3.(1)求点A的坐标及反比例函数解析式;
(2)观察图象,当y1>y2时,直接写出x的取值范围;
(3)在y轴上是否存在点P,使△ABP为直角三角形?若存在,请直接写出点P的坐标,若不存在请说明理由.
分析 (1)在y2=-x+2中,令x=0,则y2=2,得到B(0,2),根据三角形的面积S△AOB=3,求得A(3,-1),由点A是反比例函数y1=$\frac{k}{x}$(x>0)的图象上,得到k=-3,于是得到结论;
(2)根据图象即可得到x的取值范围;
(3)设P(0,a),①当∠APB=90°,由AP⊥PB,根据点A的坐标即可得到 P1(0,-1),②当∠PAB=90°,由勾股定理和两点间的距离得到方程32+(a+1)2+32+32=(2-a)2,于是得到结论.
解答 解:(1)在y2=-x+2中,令x=0,则y2=2,
∵一次函数y2=-x+2的图象与y轴相交于点B,
∴B(0,2),又∵S△AOB=3,
设A(m,n),
∴$\frac{1}{2}$×2×m=3,
∴m=3,将其代入y2=-x+2中得n=-1,
∴A(3,-1),
∵点A是反比例函数y1=$\frac{k}{x}$(x>0)的图象上,
∴k=-3,∴反比例函数解析式为:y=$\frac{-3}{x}$;
(2)由图象知:当y1>y2时,x>3;
(3)存在,设P(0,a),
①当∠APB=90°,则AP⊥PB,
∴P1(0,-1),
②当∠PAB=90°,
则AP2+AB2=PB2,
即32+(a+1)2+32+32=(2-a)2,
∴a=-4,P2(0,-4),
综上所述:P(0,-1),(0,-4).
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两个函数的解析式,两点间的距离公式,弄清题意,正确的识别图形是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
16.下列分解因式中,正确的是( )
| A. | 2x2y-xy2+xy=xy(2x-y) | B. | (x+4y)2-(2x)2=(x+4y+2x)(x+4y-2x) | ||
| C. | x3-2x2+x=x(x-1)2 | D. | 1-4x2y2=(1+4xy)(1-4xy) |
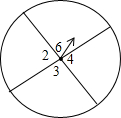 把带有指针的圆形转盘分成4等分,并且在每一区域内标上数字,小红、小明两个人玩转盘游戏,规则是:转动转盘,当转盘停止时,指针指向区域的数字是偶数,则小红胜;若指针指向区域的数字为奇数,则小明胜;若指针落在分割线上,则无效,需重新转动转盘.分别求出小红、小明获胜的概率.
把带有指针的圆形转盘分成4等分,并且在每一区域内标上数字,小红、小明两个人玩转盘游戏,规则是:转动转盘,当转盘停止时,指针指向区域的数字是偶数,则小红胜;若指针指向区域的数字为奇数,则小明胜;若指针落在分割线上,则无效,需重新转动转盘.分别求出小红、小明获胜的概率.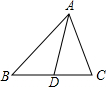 如图,在△ABC中,AD为BC边上的中线,若AB=5,AC=3,则AD的取值范围是1<AD<4.
如图,在△ABC中,AD为BC边上的中线,若AB=5,AC=3,则AD的取值范围是1<AD<4.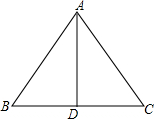 如图,在△ABC中,AB=AC,∠BAC的平分线交BC边于点D,AB=13,BC=10,则AD=12.
如图,在△ABC中,AB=AC,∠BAC的平分线交BC边于点D,AB=13,BC=10,则AD=12. 已知,如图△ABC中,AB=AC,∠A=50°,BD=CE,BF=CD,求∠FDE的度数.
已知,如图△ABC中,AB=AC,∠A=50°,BD=CE,BF=CD,求∠FDE的度数.