题目内容
19.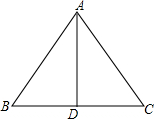 如图,在△ABC中,AB=AC,∠BAC的平分线交BC边于点D,AB=13,BC=10,则AD=12.
如图,在△ABC中,AB=AC,∠BAC的平分线交BC边于点D,AB=13,BC=10,则AD=12.
分析 由等腰三角形的性质得出AD⊥BC,BD=CD=$\frac{1}{2}$BC=5,由勾股定理求出AD即可.
解答 解:∵AB=AC,∠BAC的平分线交BC边于点D,
∴AD⊥BC,BD=CD=$\frac{1}{2}$BC=5,
∴∠ADB=90°,
∴AD=$\sqrt{{AB}^{2}-B{D}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12;
故答案为:12.
点评 本题考查了等腰三角形的性质、勾股定理;熟练掌握等腰三角形的性质,运用勾股定理进行计算是解决问题的关键.

练习册系列答案
相关题目
14.如图所示的图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.下列计算正确的是( )
| A. | (-2)-(-5)=-7 | B. | (+3)+(-6)=3 | C. | (+5)-(-8)=-3 | D. | (-5)-(-8)=3 |
9.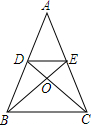 如图,DE∥BC,且S△DOE:S△BOC=4:9,则S△ADE:S△EDC等于( )
如图,DE∥BC,且S△DOE:S△BOC=4:9,则S△ADE:S△EDC等于( )
 如图,DE∥BC,且S△DOE:S△BOC=4:9,则S△ADE:S△EDC等于( )
如图,DE∥BC,且S△DOE:S△BOC=4:9,则S△ADE:S△EDC等于( )| A. | 2:3 | B. | 3:2 | C. | 2:1 | D. | 1:2 |
 二次函数y=2x2+mx+8的图象如图所示,则方程2x2+mx+8=0的根为( )
二次函数y=2x2+mx+8的图象如图所示,则方程2x2+mx+8=0的根为( )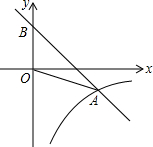 如图,平面直角坐标系中,点A是反比例函数y1=$\frac{k}{x}$(x>0)的图象上一点,一次函数y2=-x+2的图象经过点A,交y轴于点B,△AOB的面积是3.
如图,平面直角坐标系中,点A是反比例函数y1=$\frac{k}{x}$(x>0)的图象上一点,一次函数y2=-x+2的图象经过点A,交y轴于点B,△AOB的面积是3.