题目内容
2.矩形的对角线所成的角之一是65°,则对角线与各边所成的角度是( )| A. | 57.5° | B. | 32.5° | C. | 57.5°,23.5° | D. | 57.5°,32.5° |
分析 根据矩形的性质得出∠ABC=90°,AD∥BC,AB∥CD,AC=BD,AO=OC,OB=OD,推出OB=OA=OC=OD,∠OAB=∠OCD,∠DAO=∠OCB,求出∠OAD=∠ODA,∠OCB=∠OBC,∠ODC=∠OCD,根据三角形内角和定理求出即可.
解答 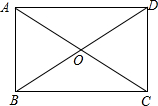
解:∵四边形ABCD是矩形,
∴∠ABC=90°,AD∥BC,AB∥CD,AC=BD,AO=OC,OB=OD,
∴OB=OA=OC=OD,∠OAB=∠OCD,∠DAO=∠OCB,
∴∠OAD=∠ODA,∠OCB=∠OBC,∠ODC=∠OCD,
∠OAB=∠OBA=$\frac{1}{2}$×(180°-∠AOB)=$\frac{1}{2}$×(180°-65°)=57.5°,
∵∠ABC=90°,
∴∠ACB=90°-57.5°=32.5°,
即∠OAD=∠ODA=∠OBC=∠OCB=32.5°,∠OAB=∠OBA=∠ODC=∠OCD=57.5°,
对角线与各边所成的角度是57.5°和32.5°,
故选D.
点评 本题考查了矩形的性质,三角形的内角和定理,等腰三角形的性质的应用,能正确运用矩形的性质进行推理是解此题的关键,注意:矩形的对角线相等且互相平分.

练习册系列答案
相关题目
13.若x<y,则下列式子正确的是( )
| A. | x-3>y-3 | B. | 3-x>3-y | C. | x+2>y+3 | D. | $\frac{x}{3}>\frac{y}{3}$ |
14.使$\frac{\sqrt{x-3}}{x-4}$有意义的x的取值范围是( )
| A. | x≥3 | B. | x≥3且x≠4 | C. | x≤3 | D. | x<3 |
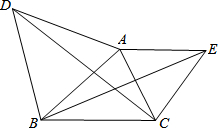 如图,△ABD、△AEC都是等边三角形.
如图,△ABD、△AEC都是等边三角形. 如图:∠B=60°,∠1=60°时,DE∥BC,理由是同位角相等,两直线平行.
如图:∠B=60°,∠1=60°时,DE∥BC,理由是同位角相等,两直线平行.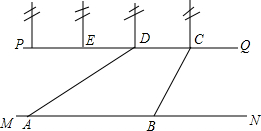 如图,河流的两岸MN,PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C,D,E…某人在河岸MN的A处测得∠DAN=30°,然后沿河岸走了120m到达B处,测得∠CBN=60°.求河流的宽度.(结果精确到0.1m)
如图,河流的两岸MN,PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C,D,E…某人在河岸MN的A处测得∠DAN=30°,然后沿河岸走了120m到达B处,测得∠CBN=60°.求河流的宽度.(结果精确到0.1m)