题目内容
12.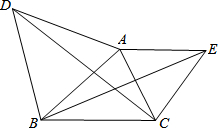 如图,△ABD、△AEC都是等边三角形.
如图,△ABD、△AEC都是等边三角形.(1)求证:BE=DC;
(2)当∠ABC=90度时,结论(1)还成立吗?
分析 (1)由等边三角形的性质得出AB=AD,AE=AC,∠BAD=∠CAE=60°,证出∠BAE=∠DAC,根据SAS证明△ABE≌△ADC,得出对应边相等即可;
(2)由等边三角形的性质得出AB=AD,AE=AC,∠BAD=∠CAE=60°,证出∠BAE=∠DAC,根据SAS证明△ABE≌△ADC,得出对应边相等即可.
解答 (1)证明:∵△ABD、△AEC都是等边三角形,
∴AB=AD,AE=AC,∠BAD=∠CAE=60°,
∴∠BAE=∠DAC,
在△ABE和△ADC中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠BAE=∠DAC}&{\;}\\{AE=AC}&{\;}\end{array}\right.$,
∴△ABE≌△ADC(SAS),
∴BE=DC;
(2)解:当∠ABC=90度时,结论(1)还成立;理由如下:如图所示: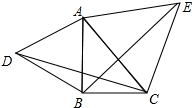 ∵△ABD、△AEC都是等边三角形,
∵△ABD、△AEC都是等边三角形,
∴AB=AD,AE=AC,∠BAD=∠CAE=60°,
∴∠BAE=∠DAC,
在△ABE和△ADC中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠BAE=∠DAC}&{\;}\\{AE=AC}&{\;}\end{array}\right.$,
∴△ABE≌△ADC(SAS),
∴BE=DC.
点评 本题考查了等边三角形的性质、全等三角形的判定与性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
20.10:30分,时针与分针的夹角是( )
| A. | 120° | B. | 135° | C. | 150° | D. | 165° |
1. 如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=36°,则∠4等于( )
如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=36°,则∠4等于( )
 如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=36°,则∠4等于( )
如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=36°,则∠4等于( )| A. | 36° | B. | 54° | C. | 72° | D. | 108° |
2.矩形的对角线所成的角之一是65°,则对角线与各边所成的角度是( )
| A. | 57.5° | B. | 32.5° | C. | 57.5°,23.5° | D. | 57.5°,32.5° |
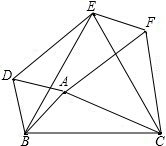 如图,分别以△ABC的三边为边长,在BC的同侧作等边△ABD,等边△BCE,等边△ACF,连接DE,EF.求证:四边形ADEF是平行四边形.
如图,分别以△ABC的三边为边长,在BC的同侧作等边△ABD,等边△BCE,等边△ACF,连接DE,EF.求证:四边形ADEF是平行四边形.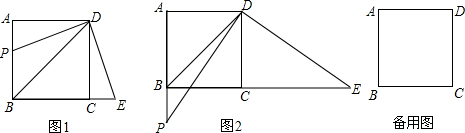
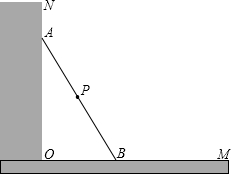 如图所示,一根长2.5米的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,此时OB的距离为0.7米,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.
如图所示,一根长2.5米的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,此时OB的距离为0.7米,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.