题目内容
7.计算:①(3$\sqrt{2}$-$\sqrt{12}$)($\sqrt{18}$$+2\sqrt{3}$)
②(2$\frac{3}{2}$-$\sqrt{\frac{1}{2}}$)×($\frac{1}{2}$$\sqrt{8}$$+\sqrt{\frac{2}{3}}$)
③$\frac{2}{y}$$\sqrt{x{y}^{5}}$(-$\frac{3}{2}$$\sqrt{{x}^{3}y}$)÷($\frac{1}{3}$$\sqrt{\frac{y}{x}}$)
④$\sqrt{12}$+$\frac{1}{2-\sqrt{3}}$-(2$+\sqrt{3}$)2.
分析 ①利用平方差公式计算;
②先把各二次根式化为最简二次根式,然后利用多项式乘多项式展开即可;
③根据二次根式的乘除法则运算;
④先利用完全平方公式计算,然后把各二次根式化为最简二次根式后合并即可.
解答 解:①原式=(3$\sqrt{2}$-2$\sqrt{3}$)(3$\sqrt{2}$+2$\sqrt{3}$)
=(3$\sqrt{2}$)2-(2$\sqrt{3}$)2
=18-12
=6;
②原式=($\frac{9}{2}$-$\frac{\sqrt{2}}{2}$)•($\sqrt{2}$+$\frac{\sqrt{6}}{3}$)
=$\frac{9\sqrt{2}}{2}$+$\frac{3\sqrt{6}}{2}$-1-$\frac{\sqrt{3}}{3}$;
③原式=$\frac{2}{y}$•(-$\frac{3}{2}$)•3•$\sqrt{x{y}^{5}•{x}^{3}y•\frac{x}{y}}$
=-9x2y$\sqrt{xy}$;
④原式=2$\sqrt{3}$+2+$\sqrt{3}$-(4+4$\sqrt{3}$+3)
=3$\sqrt{3}$+2-7-4$\sqrt{3}$
=-$\sqrt{3}$-5.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
18.下列方程中,一元二次方程是( )
| A. | ${x^2}+\frac{1}{x^2}=4$ | B. | ax2+bx-3=0 | C. | (x-1)(x+2)=1 | D. | 3x2-2xy-5y2=0 |
15. 如图,△ABC中,∠B=90°,D为BC上的一点,若∠ADC=6x°,则x可能为( )
如图,△ABC中,∠B=90°,D为BC上的一点,若∠ADC=6x°,则x可能为( )
 如图,△ABC中,∠B=90°,D为BC上的一点,若∠ADC=6x°,则x可能为( )
如图,△ABC中,∠B=90°,D为BC上的一点,若∠ADC=6x°,则x可能为( )| A. | 5 | B. | 15 | C. | 25 | D. | 35 |
12.$\frac{2x}{5x+1}$=$\frac{2x(x+4)}{(5x+1)(x+4)}$成立的条件是( )
| A. | x>-4 | B. | x<-4 | C. | x≠-4 | D. | x>0 |
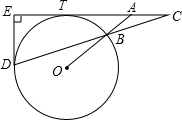 如图,已知等腰三角形ABC,AB=AC,O为AB延长线上的点,以⊙O为圆心,OB为半径作O,交CB的延长线于D,⊙O与直线AC切于点T,作DE⊥AC,垂足为E.
如图,已知等腰三角形ABC,AB=AC,O为AB延长线上的点,以⊙O为圆心,OB为半径作O,交CB的延长线于D,⊙O与直线AC切于点T,作DE⊥AC,垂足为E.
 如图,AB∥CD,∠1=40°,∠C=50°,则∠D=40°,∠B=130°.
如图,AB∥CD,∠1=40°,∠C=50°,则∠D=40°,∠B=130°.