题目内容
18．下列方程中，一元二次方程是（ ）| A． | ${x^2}+\frac{1}{x^2}=4$ | B． | ax2+bx-3=0 | C． | （x-1）（x+2）=1 | D． | 3x2-2xy-5y2=0 |
分析 根据一元二次方程的定义：未知数的最高次数是2；二次项系数不为0；是整式方程；含有一个未知数．由这四个条件对四个选项进行验证，满足这四个条件者为正确答案．
解答 解：A、是分式方程，故A错误；
B、a=0时，是一元一次方程，故B错误；
C、是一元二次方程，故意C错误；
D、是二元二次方程，故D错误；
故选：C．
点评 本题考查了一元二次方程的概念，判断一个方程是否是一元二次方程，首先要看是否是整式方程，然后看化简后是否是只含有一个未知数且未知数的最高次数是2．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．
如图，△ABC中，∠ACD=90°，AB=10，AC=6，AD平分∠BAC，DE⊥AB，垂足为点E．
（1）线段AD与CE是否垂直？说明理由．
（2）求△BDE的周长；
（3）求四边形AEDC的面积．
如图，△ABC中，∠ACD=90°，AB=10，AC=6，AD平分∠BAC，DE⊥AB，垂足为点E．（1）线段AD与CE是否垂直？说明理由．
（2）求△BDE的周长；
（3）求四边形AEDC的面积．
16．下列变形正确的有（ ）
①从13-x=-5得到-x=-5+13．
②从-7x+3=-13x-2得到13x-7x=-3-2．
③从-5x-7=2x-11得到11-7=2x-5x．
④从2x+3=3x+4得到2x-4=3x-3．
①从13-x=-5得到-x=-5+13．
②从-7x+3=-13x-2得到13x-7x=-3-2．
③从-5x-7=2x-11得到11-7=2x-5x．
④从2x+3=3x+4得到2x-4=3x-3．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
13．下列调查中适合采用抽样调查的是（ ）
| A． | 调查本班同学的视力 | |
| B． | 调查一批节能灯管的使用寿命 | |
| C． | 为保证“神舟9号”的成功发射，对其零部件进行检查 | |
| D． | 对乘坐某班次客车的乘客进行安检 |
3．下列说法错误的是（ ）
| A． | 绝对值等于本身的数只有1 | B． | a的相反数是-a | ||
| C． | 立方后等于本身的数是-1，0，1 | D． | 任何数与0相乘，都得0 |
10．我们已经研究了“圆周角”，并且知道圆周角的角度等于它所对弧的度数的一半，如图1，∠A=$\frac{\widehat{BC}的度数}{2}$．现将研究对象“顶点在圆上的角”改为“顶点在圆外的角”．定义：顶点在圆外，并且两边都和圆有公共点的角叫做圆外角，例如：图2，∠P为圆外角．
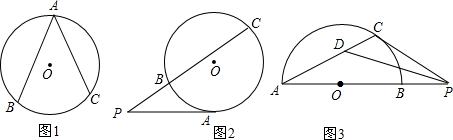
（1）如果以圆外角的两边与圆的公共点的个数作为分类标准，参照图2，请画出其它类型圆外角的示意图（要求：（请按需要选择下面的备用图，每一种类型画出一个示意图，标示相应字母，与图2同类型的不用再画）
（2）如果圆外角所夹的两条弧的度数分别为α、β（α＞β），例如，图2中，圆外角∠P所夹的弧$\widehat{AC}$的度数为α，$\widehat{AB}$的度数为β，试结合你所画的图形探究∠P与α、β之间的数量关系，将发现的结论直接写在对应图形下方的横线上．
（3）如图2，点P在⊙O外，PC边与⊙O相交于B，C两点，PA与⊙O相切于点A，所夹的弧$\widehat{AC}$，$\widehat{AB}$的度数分别为α、β（α＞β），求证：∠P=$\frac{1}{2}α-\frac{1}{2}β$．
（4）如图3，AB为半圆直径，P为AB延长线上一个动点，过P作⊙O的切线，设切点为C，连接AC，作∠APC平分线交AC于D，猜想∠CDP的度数是否随点P在AB延长线上的位置的变化而变化？并对猜想加以证明．
 ∠P=$\frac{\widehat{AmB}的度数-\widehat{AB}的度数}{2}$ | ∠P=$\frac{\widehat{AC}的度数-\widehat{AB}的度数}{2}$ | ∠P=$\frac{\widehat{CD}的度数-\widehat{AB}的度数}{2}$ |
（2）如果圆外角所夹的两条弧的度数分别为α、β（α＞β），例如，图2中，圆外角∠P所夹的弧$\widehat{AC}$的度数为α，$\widehat{AB}$的度数为β，试结合你所画的图形探究∠P与α、β之间的数量关系，将发现的结论直接写在对应图形下方的横线上．
（3）如图2，点P在⊙O外，PC边与⊙O相交于B，C两点，PA与⊙O相切于点A，所夹的弧$\widehat{AC}$，$\widehat{AB}$的度数分别为α、β（α＞β），求证：∠P=$\frac{1}{2}α-\frac{1}{2}β$．
（4）如图3，AB为半圆直径，P为AB延长线上一个动点，过P作⊙O的切线，设切点为C，连接AC，作∠APC平分线交AC于D，猜想∠CDP的度数是否随点P在AB延长线上的位置的变化而变化？并对猜想加以证明．