题目内容
19.在三张分别标有数字3,-2,0的卡片(卡片除数字不同外,其余均相同)中任选两张卡片,将所得数字分别作为点A的横纵坐标,则点A到原点的距离小于3的概率为$\frac{1}{3}$.分析 画树状图得出所有等可能的情况数,利用勾股定理找出符合要求的情况数,即可确定出所求的概率.
解答 解:画树形图得:
所有的组合为:(-2,0),(-2,3),(0,-2),(0,3),(3,-2),(3,0)共6中,
由勾股定理可知点(-2,0),(0,-2)原点的距离小于3,
所以则点A到原点的距离小于3的概率=$\frac{2}{6}$=$\frac{1}{3}$,
故答案为$\frac{1}{3}$.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
16.下列变形正确的有( )
①从13-x=-5得到-x=-5+13.
②从-7x+3=-13x-2得到13x-7x=-3-2.
③从-5x-7=2x-11得到11-7=2x-5x.
④从2x+3=3x+4得到2x-4=3x-3.
①从13-x=-5得到-x=-5+13.
②从-7x+3=-13x-2得到13x-7x=-3-2.
③从-5x-7=2x-11得到11-7=2x-5x.
④从2x+3=3x+4得到2x-4=3x-3.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.我们已经研究了“圆周角”,并且知道圆周角的角度等于它所对弧的度数的一半,如图1,∠A=$\frac{\widehat{BC}的度数}{2}$.现将研究对象“顶点在圆上的角”改为“顶点在圆外的角”.定义:顶点在圆外,并且两边都和圆有公共点的角叫做圆外角,例如:图2,∠P为圆外角.
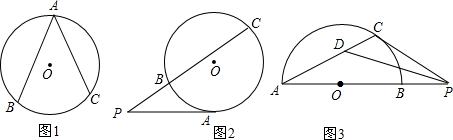
(1)如果以圆外角的两边与圆的公共点的个数作为分类标准,参照图2,请画出其它类型圆外角的示意图(要求:(请按需要选择下面的备用图,每一种类型画出一个示意图,标示相应字母,与图2同类型的不用再画)
(2)如果圆外角所夹的两条弧的度数分别为α、β(α>β),例如,图2中,圆外角∠P所夹的弧$\widehat{AC}$的度数为α,$\widehat{AB}$的度数为β,试结合你所画的图形探究∠P与α、β之间的数量关系,将发现的结论直接写在对应图形下方的横线上.
(3)如图2,点P在⊙O外,PC边与⊙O相交于B,C两点,PA与⊙O相切于点A,所夹的弧$\widehat{AC}$,$\widehat{AB}$的度数分别为α、β(α>β),求证:∠P=$\frac{1}{2}α-\frac{1}{2}β$.
(4)如图3,AB为半圆直径,P为AB延长线上一个动点,过P作⊙O的切线,设切点为C,连接AC,作∠APC平分线交AC于D,猜想∠CDP的度数是否随点P在AB延长线上的位置的变化而变化?并对猜想加以证明.

 ∠P=$\frac{\widehat{AmB}的度数-\widehat{AB}的度数}{2}$ |  ∠P=$\frac{\widehat{AC}的度数-\widehat{AB}的度数}{2}$ |  ∠P=$\frac{\widehat{CD}的度数-\widehat{AB}的度数}{2}$ |
(2)如果圆外角所夹的两条弧的度数分别为α、β(α>β),例如,图2中,圆外角∠P所夹的弧$\widehat{AC}$的度数为α,$\widehat{AB}$的度数为β,试结合你所画的图形探究∠P与α、β之间的数量关系,将发现的结论直接写在对应图形下方的横线上.
(3)如图2,点P在⊙O外,PC边与⊙O相交于B,C两点,PA与⊙O相切于点A,所夹的弧$\widehat{AC}$,$\widehat{AB}$的度数分别为α、β(α>β),求证:∠P=$\frac{1}{2}α-\frac{1}{2}β$.
(4)如图3,AB为半圆直径,P为AB延长线上一个动点,过P作⊙O的切线,设切点为C,连接AC,作∠APC平分线交AC于D,猜想∠CDP的度数是否随点P在AB延长线上的位置的变化而变化?并对猜想加以证明.
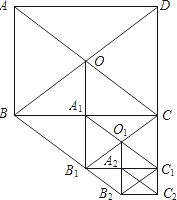 如图,在矩形ABCD中,AB=3,AD=4,以对角线的一半为边依次作平行四边形,则S${\;}_{平行四边形OB{B}_{1}C}$=6,S${\;}_{平行四边形{O}_{1}{B}_{1}{B}_{2}{C}_{1}}$=$\frac{3}{2}$.
如图,在矩形ABCD中,AB=3,AD=4,以对角线的一半为边依次作平行四边形,则S${\;}_{平行四边形OB{B}_{1}C}$=6,S${\;}_{平行四边形{O}_{1}{B}_{1}{B}_{2}{C}_{1}}$=$\frac{3}{2}$.