题目内容
2.解不等式(组),并把解集在数轴上表示出来.(1)2[x-3(x-2)]≥6($\frac{2}{3}-3x$)
(2)$\left\{\begin{array}{l}{\frac{x-3}{2}+3<x+1}\\{1-3(x-1)≤8-x}\end{array}\right.$.
分析 (1)去括号、移项、合并同类项,系数化成1即可求得不等式的解集;
(2)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
解答 解:(1)原式即2(x-3x+6)≥4-18x,
去括号,得2x-6x+12≥4-18x,
移项,得2x-6x+18x≥4-12,
合并同类项,得14x≥-8,
系数化成1得x≥-$\frac{4}{7}$.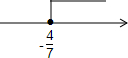 ;
;
(2)$\left\{\begin{array}{l}{\frac{x+2}{2}+3<x+1…①}\\{1-3(x-1)≤8-x…②}\end{array}\right.$,
解①得:x>6,
解②得:x≥-2. ,
,
不等式组的解集是:-2≤x<6.
点评 本题考查了不等式组的解法,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列调查中适合采用抽样调查的是( )
| A. | 调查本班同学的视力 | |
| B. | 调查一批节能灯管的使用寿命 | |
| C. | 为保证“神舟9号”的成功发射,对其零部件进行检查 | |
| D. | 对乘坐某班次客车的乘客进行安检 |
10.我们已经研究了“圆周角”,并且知道圆周角的角度等于它所对弧的度数的一半,如图1,∠A=$\frac{\widehat{BC}的度数}{2}$.现将研究对象“顶点在圆上的角”改为“顶点在圆外的角”.定义:顶点在圆外,并且两边都和圆有公共点的角叫做圆外角,例如:图2,∠P为圆外角.
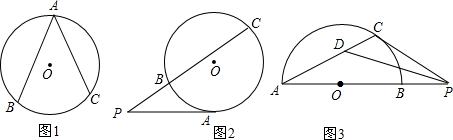
(1)如果以圆外角的两边与圆的公共点的个数作为分类标准,参照图2,请画出其它类型圆外角的示意图(要求:(请按需要选择下面的备用图,每一种类型画出一个示意图,标示相应字母,与图2同类型的不用再画)
(2)如果圆外角所夹的两条弧的度数分别为α、β(α>β),例如,图2中,圆外角∠P所夹的弧$\widehat{AC}$的度数为α,$\widehat{AB}$的度数为β,试结合你所画的图形探究∠P与α、β之间的数量关系,将发现的结论直接写在对应图形下方的横线上.
(3)如图2,点P在⊙O外,PC边与⊙O相交于B,C两点,PA与⊙O相切于点A,所夹的弧$\widehat{AC}$,$\widehat{AB}$的度数分别为α、β(α>β),求证:∠P=$\frac{1}{2}α-\frac{1}{2}β$.
(4)如图3,AB为半圆直径,P为AB延长线上一个动点,过P作⊙O的切线,设切点为C,连接AC,作∠APC平分线交AC于D,猜想∠CDP的度数是否随点P在AB延长线上的位置的变化而变化?并对猜想加以证明.

 ∠P=$\frac{\widehat{AmB}的度数-\widehat{AB}的度数}{2}$ |  ∠P=$\frac{\widehat{AC}的度数-\widehat{AB}的度数}{2}$ |  ∠P=$\frac{\widehat{CD}的度数-\widehat{AB}的度数}{2}$ |
(2)如果圆外角所夹的两条弧的度数分别为α、β(α>β),例如,图2中,圆外角∠P所夹的弧$\widehat{AC}$的度数为α,$\widehat{AB}$的度数为β,试结合你所画的图形探究∠P与α、β之间的数量关系,将发现的结论直接写在对应图形下方的横线上.
(3)如图2,点P在⊙O外,PC边与⊙O相交于B,C两点,PA与⊙O相切于点A,所夹的弧$\widehat{AC}$,$\widehat{AB}$的度数分别为α、β(α>β),求证:∠P=$\frac{1}{2}α-\frac{1}{2}β$.
(4)如图3,AB为半圆直径,P为AB延长线上一个动点,过P作⊙O的切线,设切点为C,连接AC,作∠APC平分线交AC于D,猜想∠CDP的度数是否随点P在AB延长线上的位置的变化而变化?并对猜想加以证明.
12.A为反比例函数$y=\frac{k}{x}$(k<0)图象上一点,AB垂直x轴,垂足为B点,若S△AOB=3,则k的值为( )
| A. | 6 | B. | -6 | C. | $\frac{3}{2}$ | D. | 不能确定 |