题目内容
15．
如图，△ABC中，∠B=90°，D为BC上的一点，若∠ADC=6x°，则x可能为（ ）| A． | 5 | B． | 15 | C． | 25 | D． | 35 |
分析 根据三角形的外角的性质得到∠ADC=∠B+∠BAD，得到6x＞90，根据平角的概念得到6x＜180，计算后进行判断得到答案．
解答 解：∵∠ADC=∠B+∠BAD，
∴6x＞90，
解得，x＞15，
又6x＜180，
解得，x＜30，
故选：C．
点评 本题考查的是三角形的外角的性质，掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键．
练习册系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
3．下列说法错误的是（ ）
| A． | 绝对值等于本身的数只有1 | B． | a的相反数是-a | ||
| C． | 立方后等于本身的数是-1，0，1 | D． | 任何数与0相乘，都得0 |
10．我们已经研究了“圆周角”，并且知道圆周角的角度等于它所对弧的度数的一半，如图1，∠A=$\frac{\widehat{BC}的度数}{2}$．现将研究对象“顶点在圆上的角”改为“顶点在圆外的角”．定义：顶点在圆外，并且两边都和圆有公共点的角叫做圆外角，例如：图2，∠P为圆外角．
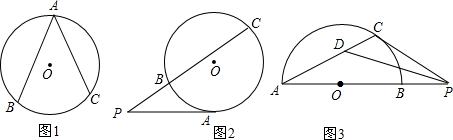
（1）如果以圆外角的两边与圆的公共点的个数作为分类标准，参照图2，请画出其它类型圆外角的示意图（要求：（请按需要选择下面的备用图，每一种类型画出一个示意图，标示相应字母，与图2同类型的不用再画）
（2）如果圆外角所夹的两条弧的度数分别为α、β（α＞β），例如，图2中，圆外角∠P所夹的弧$\widehat{AC}$的度数为α，$\widehat{AB}$的度数为β，试结合你所画的图形探究∠P与α、β之间的数量关系，将发现的结论直接写在对应图形下方的横线上．
（3）如图2，点P在⊙O外，PC边与⊙O相交于B，C两点，PA与⊙O相切于点A，所夹的弧$\widehat{AC}$，$\widehat{AB}$的度数分别为α、β（α＞β），求证：∠P=$\frac{1}{2}α-\frac{1}{2}β$．
（4）如图3，AB为半圆直径，P为AB延长线上一个动点，过P作⊙O的切线，设切点为C，连接AC，作∠APC平分线交AC于D，猜想∠CDP的度数是否随点P在AB延长线上的位置的变化而变化？并对猜想加以证明．
 ∠P=$\frac{\widehat{AmB}的度数-\widehat{AB}的度数}{2}$ | ∠P=$\frac{\widehat{AC}的度数-\widehat{AB}的度数}{2}$ | ∠P=$\frac{\widehat{CD}的度数-\widehat{AB}的度数}{2}$ |
（2）如果圆外角所夹的两条弧的度数分别为α、β（α＞β），例如，图2中，圆外角∠P所夹的弧$\widehat{AC}$的度数为α，$\widehat{AB}$的度数为β，试结合你所画的图形探究∠P与α、β之间的数量关系，将发现的结论直接写在对应图形下方的横线上．
（3）如图2，点P在⊙O外，PC边与⊙O相交于B，C两点，PA与⊙O相切于点A，所夹的弧$\widehat{AC}$，$\widehat{AB}$的度数分别为α、β（α＞β），求证：∠P=$\frac{1}{2}α-\frac{1}{2}β$．
（4）如图3，AB为半圆直径，P为AB延长线上一个动点，过P作⊙O的切线，设切点为C，连接AC，作∠APC平分线交AC于D，猜想∠CDP的度数是否随点P在AB延长线上的位置的变化而变化？并对猜想加以证明．
20．下列说法正确的是（ ）
| A． | 若a＞b，则ac2＞bc2 | B． | 若ac2＞bc2，则a＞b | C． | 若a＞b，则a2＞b2 | D． | 若a＞b，则$\frac{1}{a}$＜$\frac{1}{b}$ |
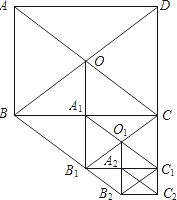如图，在矩形ABCD中，AB=3，AD=4，以对角线的一半为边依次作平行四边形，则S${\;}_{平行四边形OB{B}_{1}C}$=6，S${\;}_{平行四边形{O}_{1}{B}_{1}{B}_{2}{C}_{1}}$=$\frac{3}{2}$．