题目内容
4.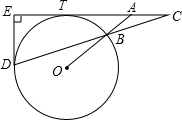 如图,已知等腰三角形ABC,AB=AC,O为AB延长线上的点,以⊙O为圆心,OB为半径作O,交CB的延长线于D,⊙O与直线AC切于点T,作DE⊥AC,垂足为E.
如图,已知等腰三角形ABC,AB=AC,O为AB延长线上的点,以⊙O为圆心,OB为半径作O,交CB的延长线于D,⊙O与直线AC切于点T,作DE⊥AC,垂足为E.(1)求证:DE是⊙O的切线;
(2)若⊙O的半径r=3,CE=9,求AB的长.
分析 (1)连接OD,根据等腰三角形的性质即可求得∠C=∠ODB,进而求得∠C+∠EDC=∠ODB+∠EDC=90°,即∠ODE=90°,即可证得DE是⊙O的切线;
(2)连接OT,证得四边形ODET是正方形,得出DE=ET=r=3,设AB=AC=x,则AT=9-3-x=6-x,OA=r+x=3+x,然后根据勾股定理得出(3+x)=32+(6-x)2,解方程即可求得AB的长.
解答  (1)证明:连接OD,
(1)证明:连接OD,
∵AB=AC,OB=OD,
∴∠C=∠ABC,∠OBD=∠ODB,
∵∠ABC=∠OBD,
∴∠C=∠ODB,
∵DE⊥AC,
∴∠C+∠EDC=90°,
∴∠ODB+∠EDC=90°,
即∠ODE=90°,
∴DE是⊙O的切线;
(2)解:连接OT,
∵⊙O与直线AC切于点T,
∴OT⊥AE,
∵∠ODC=∠E=90°,
∴四边形ODET是矩形,
∵OD=OT,
∴四边形ODET是正方形,
∴DE=ET=r=3,
设AB=AC=x,则AT=EC-ET-AC=9-3-x=6-x,OA=r+x=3+x,
在RT△OAT中,OA2=OT2+TA2,
即(3+x)=32+(6-x)2,
解得x=2,
∴AB=2.
点评 本题考查了切线的判定和性质,等腰三角形的性质以及正方形的判定和性质,勾股定理的应用等,作出辅助线,证得四边形ODET是正方形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.作图题:
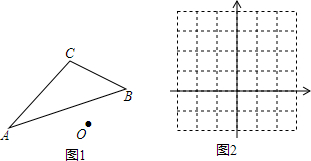
(1)请在图1中作出△ABC关于点O对称的△A′B′C′(不写作法,但要保留作图痕迹)
(2)画二次函数y=$\frac{1}{2}$x2的图象.
解:①列表如下(补充完成下表)
②描点(请在图中描出上表中的点)
③连线(在图中连线,画出y=$\frac{1}{2}$x2的图象)即为所求.

(1)请在图1中作出△ABC关于点O对称的△A′B′C′(不写作法,但要保留作图痕迹)
(2)画二次函数y=$\frac{1}{2}$x2的图象.
解:①列表如下(补充完成下表)
| x | … | -2 | -1 | 0 | 1 | … | |
| y | … | 0.5 | 0 | 0.5 | 2 | … |
③连线(在图中连线,画出y=$\frac{1}{2}$x2的图象)即为所求.
15. 如图,△ABC中,∠ACD=90°,AB=10,AC=6,AD平分∠BAC,DE⊥AB,垂足为点E.
如图,△ABC中,∠ACD=90°,AB=10,AC=6,AD平分∠BAC,DE⊥AB,垂足为点E.
(1)线段AD与CE是否垂直?说明理由.
(2)求△BDE的周长;
(3)求四边形AEDC的面积.
 如图,△ABC中,∠ACD=90°,AB=10,AC=6,AD平分∠BAC,DE⊥AB,垂足为点E.
如图,△ABC中,∠ACD=90°,AB=10,AC=6,AD平分∠BAC,DE⊥AB,垂足为点E.(1)线段AD与CE是否垂直?说明理由.
(2)求△BDE的周长;
(3)求四边形AEDC的面积.
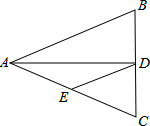 如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )