题目内容
20.已知抛物线y=$\frac{1}{2}$x2+c与x轴交于A(-1,0),B两点,交y轴于点C.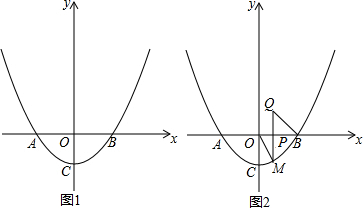
(1)求抛物线的解析式;
(2)点E(m,n)是第二象限内一点,过点E作EF⊥x轴交抛物线于点F,过点F作FG⊥y轴于点G,连接CE、CF,若∠CEF=∠CFG.求n的值并直接写出m的取值范围(利用图1完成你的探究).
(3)如图2,点P是线段OB上一动点(不包括点O、B),PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,BQ交直线PM于点Q,设点P的横坐标为t,求△PBQ的周长.
分析 (1)将点A的坐标代入抛物线解析式即可求得c的值,则可得抛物线解析式;
(2)过点C作CH⊥EF于点H,易证△EHC∽△FGC,再根据相似三角形的性质可得n的值;
(3)首先表示出点P的坐标,再根据△OPM∽△QPB,然后由对应边的比值相等得出PQ和BQ的长,从而可得△PBQ的周长.
解答 解:(1)把A(-1,0)代入$y=\frac{1}{2}{x}^{2}+c$
得c=-$\frac{1}{2}$,
∴抛物线解析式为$y=\frac{1}{2}{x}^{2}-\frac{1}{2}$
(2)如图1,过点C作CH⊥EF于点H,
∵∠CEF=∠CFG,FG⊥y轴于点G
∴△EHC∽△FGC
∵E(m,n)
∴F(m,$\frac{1}{2}{m}^{2}-\frac{1}{2}$)
又∵C(0,-$\frac{1}{2}$)
∴EH=n+$\frac{1}{2}$,CH=-m,FG=-m,CG=$\frac{1}{2}$m2
又∵$\frac{EH}{CH}=\frac{FG}{CG}$,
则$\frac{n+\frac{1}{2}}{-m}=\frac{-m}{\frac{1}{2}{m}^{2}}$
∴n+$\frac{1}{2}$=2
∴n=$\frac{3}{2}$
当F点位于E点上方时,则∠CEF>90°;又∠CFG肯定为锐角,故这种情形不符合题意.
由此当n=$\frac{3}{2}$时,代入抛物线解析式,求得m=±2,
又E点位于第二象限,所以-2<m<0.
(3)由题意可知P(t,0),M(t,$\frac{1}{2}{t}^{2}-\frac{1}{2}$)
∵PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,
∴△OPM∽△QPB.
∴$\frac{OP}{PM}=\frac{PQ}{PB}$.
其中OP=t,PM=$\frac{1}{2}-\frac{1}{2}{t}^{2}$,PB=1-t,
∴PQ=$\frac{2t}{1+t}$.
BQ=$\sqrt{P{B}^{2}+P{Q}^{2}}=\frac{{t}^{2}+1}{t+1}$
∴PQ+BQ+PB=$\frac{2t}{1+t}+\frac{{t}^{2}+1}{1+t}+1-t=2$.
∴△PBQ的周长为2.
点评 本题考查了二次函数的综合应用,同时涉及了相似三角形的判定与性质,具有一定的综合性与难度,解题时要注意数形结合思想与方程思想的运用.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案| A. | (3,2) | B. | (2,-3) | C. | (-3,-2) | D. | (3,-2) |
 已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )| A. | |a|<1<|b| | B. | 1<-a<b | C. | 1<|a|<b | D. | -b<a<-1 |
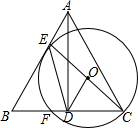 如图,在△ABC中,AB=AC,AD⊥BC于点D,E为边AB上一点,ED=CD,以CE为直径作⊙O,交BC于点F.
如图,在△ABC中,AB=AC,AD⊥BC于点D,E为边AB上一点,ED=CD,以CE为直径作⊙O,交BC于点F.
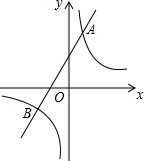 如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).
如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).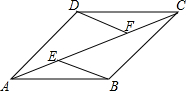 已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.
已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.