题目内容
11.如果$\frac{a}{b}$=3,那么代数式$\frac{{a}^{2}-ab+{b}^{2}}{{a}^{2}+{b}^{2}}$的值等于$\frac{7}{10}$.分析 先根据题意得出a=3b,再由分式混合运算的法则把原式进行化简,把a=3b代入进行计算即可.
解答 解:∵$\frac{a}{b}$=3,
∴a=3b.
∴原式=$\frac{{(a}^{2}+{b}^{2})-ab}{{a}^{2}+{b}^{2}}$=1-$\frac{ab}{{a}^{2}+{b}^{2}}$=1-$\frac{3{b}^{2}}{9{b}^{2}+{b}^{2}}$=$\frac{7}{10}$.
故答案为:$\frac{7}{10}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
1.下列运算中,正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | -a+2a=a | C. | (a3)3=a6 | D. | $\root{3}{27}$=-3 |
3.已知抛物线y=ax2+bx+c(a>0)过(-2,0),(2,3)两点,那么抛物线的对称轴( )
| A. | 只能是x=-1 | |
| B. | 可能是y轴 | |
| C. | 可能在y轴右侧且在直线x=2的左侧 | |
| D. | 可能在y轴左侧且在直线x=-2的右侧 |
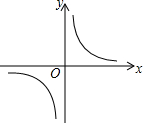 反比例函数y=$\frac{m}{x}$的图象如图所示,以下结论:
反比例函数y=$\frac{m}{x}$的图象如图所示,以下结论: 如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m).
如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m).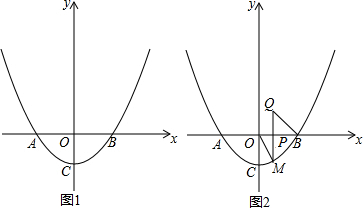
 如图,△ABC是直角三角形,∠ACB=90°.
如图,△ABC是直角三角形,∠ACB=90°.