题目内容
15．在平面直角坐标系中，把点P（-3，2）绕原点O顺时针旋转180°，所得到的对应点P′的坐标为（ ）| A． | （3，2） | B． | （2，-3） | C． | （-3，-2） | D． | （3，-2） |
分析 将点P绕原点O顺时针旋转180°，实际上是求点P关于原点的对称点的坐标．
解答 解：根据题意得，点P关于原点的对称点是点P′，
∵P点坐标为（-3，2），
∴点P′的坐标（3，-2）．
故选：D．
点评 本题考查了坐标与图形的变换-旋转，熟练掌握关于原点的对称点的坐标特征是解决问题的关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
3．已知抛物线y=ax2+bx+c（a＞0）过（-2，0），（2，3）两点，那么抛物线的对称轴（ ）
| A． | 只能是x=-1 | |
| B． | 可能是y轴 | |
| C． | 可能在y轴右侧且在直线x=2的左侧 | |
| D． | 可能在y轴左侧且在直线x=-2的右侧 |
如图，抛物线y=-x2+2x+m+1交x轴于点A（a，0）和B（b，0），交y轴于点C，抛物线的顶点为D，下列四个命题：
7．
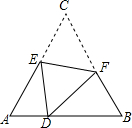如图，D是等边△ABC边AB上的一点，且AD：DB=1：2，现将△ABC折叠，使点C与D重合，折痕为EF，点E，F分别在AC和BC上，则CE：CF=（ ）
如图，D是等边△ABC边AB上的一点，且AD：DB=1：2，现将△ABC折叠，使点C与D重合，折痕为EF，点E，F分别在AC和BC上，则CE：CF=（ ）| A． | $\frac{3}{4}$ | B． | $\frac{4}{5}$ | C． | $\frac{5}{6}$ | D． | $\frac{6}{7}$ |
4．
如图，将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上．如果∠2=60°，那么∠1的度数为（ ）
如图，将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上．如果∠2=60°，那么∠1的度数为（ ）| A． | 60° | B． | 50° | C． | 40° | D． | 30° |
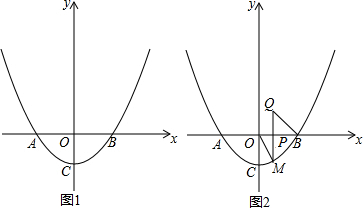
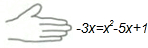老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了如图所示的一个二次三项式，形式如图：