题目内容
10.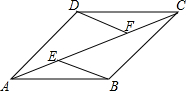 已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.
已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.求证:四边形ABCD为菱形.
分析 首先证得△ABE≌△CDF,得到AB=CD,从而得到四边形ABCD是平行四边形,然后证得AD=CD,利用邻边相等的平行四边形是菱形进行证明即可.
解答 证明:∵AB∥CD,
∴∠DCA=∠BAC,
∵DF∥BE,
∴∠DFA=∠BEC,
∴∠AEB=∠CFD,
在△AEB和△CFD中,$\left\{\begin{array}{l}{∠DCF=∠EAB}\\{AE=CF}\\{∠AEB=∠CFD}\end{array}\right.$,
∴△AEB≌△CFD(ASA),
∴AB=CD,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AC平分∠BAD,
∴∠BAE=∠DAF,
∵∠BAE=∠DCF,
∴∠DAF=∠DCF,
∴AD=CD,
∴四边形ABCD是菱形.
点评 本题考查了菱形的判定,能够了解菱形的几种判定方法是解答本题的关键,难度不大.

练习册系列答案
相关题目
18. 在数轴上标注了四段范围,如图,则表示$\sqrt{8}$的点落在( )
在数轴上标注了四段范围,如图,则表示$\sqrt{8}$的点落在( )
 在数轴上标注了四段范围,如图,则表示$\sqrt{8}$的点落在( )
在数轴上标注了四段范围,如图,则表示$\sqrt{8}$的点落在( )| A. | 段① | B. | 段② | C. | 段③ | D. | 段④ |
20. 如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=70°,则∠2=( )
如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=70°,则∠2=( )
 如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=70°,则∠2=( )
如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=70°,则∠2=( )| A. | 70° | B. | 80° | C. | 110° | D. | 120° |
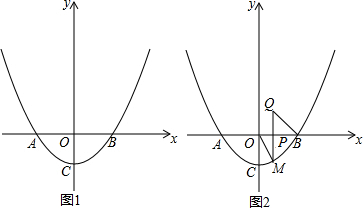
 如图,△ABC是直角三角形,∠ACB=90°.
如图,△ABC是直角三角形,∠ACB=90°.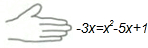 老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了如图所示的一个二次三项式,形式如图:
老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了如图所示的一个二次三项式,形式如图: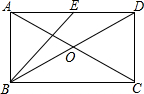 如图,在矩形ABCD中,对角线AC,BD相交于点O,E是边AD的中点.若AC=10,DC=2$\sqrt{5}$,则BO=5,∠EBD的大小约为18度26分.(参考数据:tan26°34′≈$\frac{1}{2}$)
如图,在矩形ABCD中,对角线AC,BD相交于点O,E是边AD的中点.若AC=10,DC=2$\sqrt{5}$,则BO=5,∠EBD的大小约为18度26分.(参考数据:tan26°34′≈$\frac{1}{2}$)