题目内容
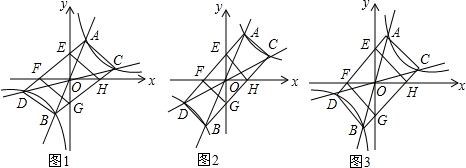
5.已知△ABC,AB=AC,将△ABC沿BC方向平移得到△DEF.(1)如图1,连接BD,AF,则BD=AF(填“>”、“<”或“=”);
(2)如图2,M为AB边上一点,过M作BC的平行线MN分别交边AC,DE,DF于点G,H,N,连接BH,GF,求证:BH=GF.
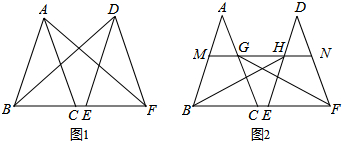
分析 (1)根据等腰三角形的性质,可得∠ABC与∠ACB的关系,根据平移的性质,可得AC与DF的关系,根据全等三角形的判定与性质,可得答案;
(2)根据相似三角形的判定与性质,可得GM与HN的关系,BM与FN的关系,根据全等三角形的判定与性质,可得答案.
解答 (1)解:由AB=AC,
得∠ABC=ACB.
由△ABC沿BC方向平移得到△DEF,
得DF=AC,∠DFE=∠ACB.
在△ABF和△DFB中,
$\left\{\begin{array}{l}{AB=DF}\\{∠ABF=∠DFB}\\{BF=FB}\end{array}\right.$,
△ABF≌△DFB(SAS),
BD=AF,
故答案为:BD=AF;
(2)证明:如图: ,
,
MN∥BF,
△AMG∽△ABC,△DHN∽△DEF,
$\frac{MG}{BC}$=$\frac{AM}{AB}$=$\frac{ND}{DF}$,$\frac{HN}{EF}$=$\frac{DN}{DF}$,
∴MG=HN,MB=NF.
在△BMH和△FNG中,
$\left\{\begin{array}{l}{BM=FN}\\{∠BMH=∠FNG}\\{MH=NG}\end{array}\right.$,
△BMH≌△FNG(SAS),
∴BH=FG.
点评 本题考查了全等三角形的判定与性质,利用了平移的性质,相似三角形的判定与性质,全等三角形的判定与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.在-2,1,2,1,4,6中正确的是( )
| A. | 平均数3 | B. | 众数是-2 | C. | 极差为8 | D. | 中位数是1 |
10.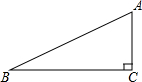 如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
 如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )| A. | 5÷tan26°= | B. | 5÷sin26°= | C. | 5×cos26°= | D. | 5×tan26°= |
 如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m).
如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m).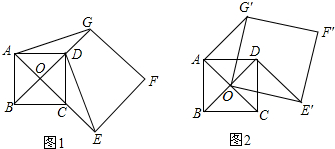
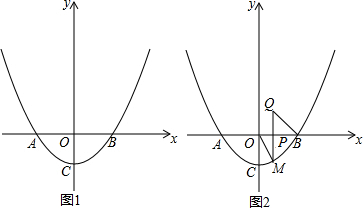
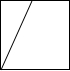
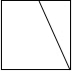
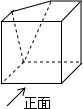 如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为( )
如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为( )

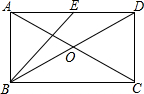 如图,在矩形ABCD中,对角线AC,BD相交于点O,E是边AD的中点.若AC=10,DC=2$\sqrt{5}$,则BO=5,∠EBD的大小约为18度26分.(参考数据:tan26°34′≈$\frac{1}{2}$)
如图,在矩形ABCD中,对角线AC,BD相交于点O,E是边AD的中点.若AC=10,DC=2$\sqrt{5}$,则BO=5,∠EBD的大小约为18度26分.(参考数据:tan26°34′≈$\frac{1}{2}$)