题目内容
10.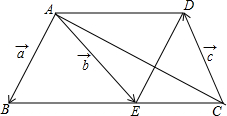 如图,在梯形ABCD中,AD∥BC,点E在边BC上,DE∥AB,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AE}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$.
如图,在梯形ABCD中,AD∥BC,点E在边BC上,DE∥AB,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AE}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$.(1)试用向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$表示下列向量:$\overrightarrow{AD}$,$\overrightarrow{CE}$,$\overrightarrow{AC}$.
(2)求作:$\overrightarrow{b}$-$\overrightarrow{a}$+$\overrightarrow{c}$.(保留作图痕迹,写出结果,不要求写作法)
分析 (1)AD∥BC,DE∥AB,可证得四边形ABED是平行四边形,然后利用平行四边形法则与三角形法则求解即可求得答案;
(2)首先作$\overrightarrow{DF}$=$\overrightarrow{c}$,连接AF,则$\overrightarrow{AF}$即为所求.
解答 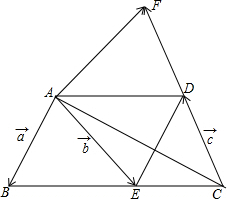 解:(1)∵AD∥BC,DE∥AB,
解:(1)∵AD∥BC,DE∥AB,
∴四边形ABED是平行四边形,
∴$\overrightarrow{AD}$=$\overrightarrow{BE}$=$\overrightarrow{AE}$-$\overrightarrow{AB}$=$\overrightarrow{b}$-$\overrightarrow{a}$,$\overrightarrow{DE}$=$\overrightarrow{AB}$=$\overrightarrow{a}$,
∴$\overrightarrow{CE}$=$\overrightarrow{CD}$+$\overrightarrow{DE}$=$\overrightarrow{c}$+$\overrightarrow{a}$;
∴$\overrightarrow{BC}$=$\overrightarrow{BE}$-$\overrightarrow{CE}$=($\overrightarrow{b}$-$\overrightarrow{a}$)-($\overrightarrow{c}$+$\overrightarrow{a}$)=$\overrightarrow{b}$-$\overrightarrow{c}$-2$\overrightarrow{a}$,
∴$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{a}$+($\overrightarrow{b}$-$\overrightarrow{c}$-2$\overrightarrow{a}$)=$\overrightarrow{b}$-$\overrightarrow{c}$-$\overrightarrow{a}$;
(2)如图,作$\overrightarrow{DF}$=$\overrightarrow{c}$,连接AF,则$\overrightarrow{AF}$即为所求.
点评 此题考查了平面向量的知识.注意掌握平行四边形法则与三角形法则是解此题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,利用直尺和三角尺作平行线,其依据是( )
如图,利用直尺和三角尺作平行线,其依据是( )| A. | 同位角相等,两直线平行 | B. | 内错角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 两直线平行,同位角相等 |
| A. | -8 | B. | -6 | C. | 6 | D. | 8 |
| A. | 18 | B. | 12 | C. | 9 | D. | 7 |
| A. | $\frac{33}{100}$ | B. | $\frac{34}{100}$ | C. | $\frac{3}{10}$ | D. | 无法确定 |
①同位角相等;②在△ABC中,若∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C,△ABC是直角三角形;③两条对角线互相垂直的四边形是菱形;④平分弦的直径垂直于弦,并且平分弦所对的弧.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
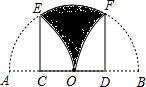 如图,在以点O为圆心的半圆中,AB为直径,且AB=4,将该半圆折叠,使点A和点B落在点O处,折痕分别为EC和FD,则图中阴影部分面积为( )
如图,在以点O为圆心的半圆中,AB为直径,且AB=4,将该半圆折叠,使点A和点B落在点O处,折痕分别为EC和FD,则图中阴影部分面积为( )| A. | 4$\sqrt{3}$-$\frac{π}{3}$ | B. | 4$\sqrt{3}$-$\frac{2π}{3}$ | C. | 2$\sqrt{3}$-$\frac{π}{3}$ | D. | 2$\sqrt{3}$-$\frac{2π}{3}$ |