题目内容
18.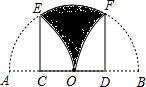 如图,在以点O为圆心的半圆中,AB为直径,且AB=4,将该半圆折叠,使点A和点B落在点O处,折痕分别为EC和FD,则图中阴影部分面积为( )
如图,在以点O为圆心的半圆中,AB为直径,且AB=4,将该半圆折叠,使点A和点B落在点O处,折痕分别为EC和FD,则图中阴影部分面积为( )| A. | 4$\sqrt{3}$-$\frac{π}{3}$ | B. | 4$\sqrt{3}$-$\frac{2π}{3}$ | C. | 2$\sqrt{3}$-$\frac{π}{3}$ | D. | 2$\sqrt{3}$-$\frac{2π}{3}$ |
分析 根据题意求得AC=OC=OD=DB=1,CD=2,EC=$\sqrt{O{E}^{2}-O{C}^{2}}$=$\sqrt{3}$,进一步求得△EOF是等边三角形,然后根据S阴影=S长方形-(S半圆-S长方形CDFE)+2(S扇形OEF-S△EOF)即可求得.
解答 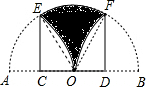 解:∵AB为直径,且AB=4,
解:∵AB为直径,且AB=4,
∴OA=OE=2,
∵点A和点B落在点O处,折痕分别为EC和FD,
∴AC=OC=OD=DB=1,
∴CD=2,EC=$\sqrt{O{E}^{2}-O{C}^{2}}$=$\sqrt{3}$,
∴△EOF是等边三角形,
∴∠EOF=60°,
∴S半圆=$\frac{1}{2}$π×22=2π,S长方形CDFE=2×$\sqrt{3}$=2$\sqrt{3}$,
∴S阴影=S长方形-(S半圆-S长方形CDFE)+2(S扇形OEF-S△EOF)
=4$\sqrt{3}$-2π+2($\frac{2π}{3}$-$\frac{1}{2}$×2×$\sqrt{3}$)
=2$\sqrt{3}$-$\frac{2π}{3}$.
故选D.
点评 本题考查了不规则图形面积的计算方法:把不规则的图形面积的计算转化为规则图形的面积和差来计算.也考查了等边三角形的判定和性质以及勾股定理.

练习册系列答案
相关题目
11.在下列调查中,适宜采用普查的是( )
| A. | 了解某校九(1)班学生视力情况 | B. | 调查2016年央视春晚的收视率 | ||
| C. | 检测一批电灯泡的使用寿命 | D. | 了解我市中学生课余上网时间 |
8.下列运算正确的是( )
| A. | $\sqrt{4}=±2$ | B. | (-1)2016=-1 | C. | (-3)-2=6 | D. | (-2)3÷(-2)2=-2 |
3.若关于x的方程x2-4x+k=0的一个根为2-$\sqrt{3}$,则k的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
10.已知二次函数y=2x2-4x-3,若函数值y随x的增大而减小,则x的取值范围是( )
| A. | x≤1 | B. | x≥1 | C. | x≥-2 | D. | -2≤x<4 |
5.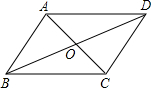 如图,?ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
如图,?ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
 如图,?ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
如图,?ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )| A. | 13 | B. | 17 | C. | 20 | D. | 26 |
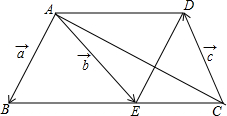 如图,在梯形ABCD中,AD∥BC,点E在边BC上,DE∥AB,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AE}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$.
如图,在梯形ABCD中,AD∥BC,点E在边BC上,DE∥AB,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AE}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$.


