题目内容
2.已知$\frac{a}{2}=\frac{b}{3}≠0$,求代数式$\frac{a}{a+2b}-\frac{{4{b^2}}}{{{a^2}+2ab}}$的值.分析 先通分,再把分子相加减,由$\frac{a}{2}$=$\frac{b}{3}$可设a=2k,b=3k,再代入代数式进行计算即可.
解答 解:原式=$\frac{a}{a+2b}$-$\frac{4{b}^{2}}{{a}^{2}+2ab}$
=$\frac{{a}^{2}}{a(a+2b)}$-$\frac{4{b}^{2}}{a(a+2b)}$
=$\frac{a-2b}{a}$,
∵$\frac{a}{2}$=$\frac{b}{3}$≠0,
∴设a=2k,则b=3k.
∴原式=-2.
点评 本题考查的是分式的化简求值,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
13.下列数据不能确定物体位置的是( )
| A. | 2楼4号 | B. | 大学路19号 | C. | 北偏东60° | D. | 东经111°北纬40° |
14.方程x2-2x-3=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有且只有一个实数根 | D. | 没有实数根 |
17.在平面直角坐标系中,将点(-2,3)关于原点的对称点向右平移2个单位长度得到的点的坐标是( )
| A. | (4,-3) | B. | (-4,3) | C. | (0,-3) | D. | (0,3) |
7. “奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )
“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )
 “奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )
“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )| A. | 30$\sqrt{3}$m | B. | 20$\sqrt{5}$m | C. | 30$\sqrt{2}$m | D. | 15$\sqrt{6}$m |
14.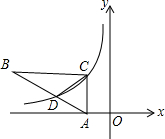 如图Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )
如图Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )
 如图Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )
如图Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )| A. | 3 | B. | 6 | C. | -3 | D. | -6 |
11.在下列调查中,适宜采用普查的是( )
| A. | 了解某校九(1)班学生视力情况 | B. | 调查2016年央视春晚的收视率 | ||
| C. | 检测一批电灯泡的使用寿命 | D. | 了解我市中学生课余上网时间 |
10.已知二次函数y=2x2-4x-3,若函数值y随x的增大而减小,则x的取值范围是( )
| A. | x≤1 | B. | x≥1 | C. | x≥-2 | D. | -2≤x<4 |
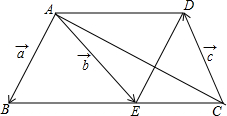 如图,在梯形ABCD中,AD∥BC,点E在边BC上,DE∥AB,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AE}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$.
如图,在梯形ABCD中,AD∥BC,点E在边BC上,DE∥AB,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AE}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$.