题目内容
15.从标有号数1到100的100张卡片中,随意抽取一张,其号数为3的倍数的概率是( )| A. | $\frac{33}{100}$ | B. | $\frac{34}{100}$ | C. | $\frac{3}{10}$ | D. | 无法确定 |
分析 由从标有号数1到100的100张卡片中,随意抽取一张,其号数为3的倍数的有33个,直接利用概率公式求解即可求得答案.
解答 解:∵从标有号数1到100的100张卡片中,随意抽取一张,其号数为3的倍数的有33个,
∴随意抽取一张,其号数为3的倍数的概率是:$\frac{33}{100}$.
故选A.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
3.若一个不透明的袋子中装有2个白球、3个黄球和1个红球,这些球除颜色外其他完全相同,则从袋子中随机摸出一个球是白球的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
7. “奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )
“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )
 “奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )
“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )| A. | 30$\sqrt{3}$m | B. | 20$\sqrt{5}$m | C. | 30$\sqrt{2}$m | D. | 15$\sqrt{6}$m |
4.已知抛物线y=-$\frac{1}{6}{x}^{2}+\frac{3}{2}x+6$与直线y=x交于点A,点B,则AB的长为( )
| A. | 3$\sqrt{34}$ | B. | 6$\sqrt{17}$ | C. | 3$\sqrt{17}$ | D. | 2$\sqrt{34}$ |
3.若关于x的方程x2-4x+k=0的一个根为2-$\sqrt{3}$,则k的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
 某市有A、B、C、D四个大型超市,分别位于一条东西走向的平安大路两侧,如图,若C(-2,8)、D(0,0),请建立适当的直角坐标系,并写出A、B两个超市相应的坐标.
某市有A、B、C、D四个大型超市,分别位于一条东西走向的平安大路两侧,如图,若C(-2,8)、D(0,0),请建立适当的直角坐标系,并写出A、B两个超市相应的坐标.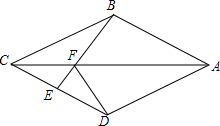 如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.
如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.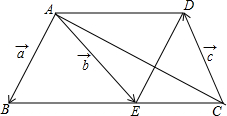 如图,在梯形ABCD中,AD∥BC,点E在边BC上,DE∥AB,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AE}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$.
如图,在梯形ABCD中,AD∥BC,点E在边BC上,DE∥AB,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AE}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$. 如图,在△ABC中,AB=4,将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1,则阴影部分的面积为4.
如图,在△ABC中,AB=4,将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1,则阴影部分的面积为4.