题目内容
5.已知x2+x-3=0,求代数式$\frac{{{x^2}-1}}{{{x^2}-2x+1}}•\frac{1}{x+1}+\frac{x+1}{x+2}$的值.分析 先算乘法,再算加减,根据x2+x-3=0得出x2+x=3,代入代数式进行计算即可.
解答 解:原式=$\frac{(x+1)(x-1)}{{(x-1)}^{2}}$•$\frac{1}{x+1}$+$\frac{x+1}{x+2}$
=$\frac{1}{x-1}$+$\frac{x+1}{x+2}$
=$\frac{x+2}{(x-1)(x+2)}$+$\frac{(x-1)(x+1)}{(x-1)(x+2)}$
=$\frac{{{x^2}+x+1}}{{{x^2}+x-2}}$.
∵x2+x-3=0
∴x2+x=3
∴原式=$\frac{{{x^2}+x+1}}{{{x^2}+x-2}}=\frac{3+1}{3-2}=4$.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.

练习册系列答案
相关题目
16.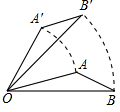 如图,将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )
如图,将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )
 如图,将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )
如图,将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
14.方程x2-2x-3=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有且只有一个实数根 | D. | 没有实数根 |
17.在平面直角坐标系中,将点(-2,3)关于原点的对称点向右平移2个单位长度得到的点的坐标是( )
| A. | (4,-3) | B. | (-4,3) | C. | (0,-3) | D. | (0,3) |
 如图,将△ABC绕点B顺时针旋转40°得到△DBE,若此时点A的对应点D恰好落在边AC上,且∠ABE=90°,则∠C的度数为60°.
如图,将△ABC绕点B顺时针旋转40°得到△DBE,若此时点A的对应点D恰好落在边AC上,且∠ABE=90°,则∠C的度数为60°.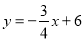 与
与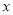 轴、
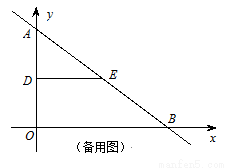
轴、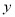 轴分别交于点B、 A,点D、E分别是AO、AB的中点,连接DE,点P从点D出发,沿DE方向匀速运动,速度为1cm/s;与此同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为
轴分别交于点B、 A,点D、E分别是AO、AB的中点,连接DE,点P从点D出发,沿DE方向匀速运动,速度为1cm/s;与此同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为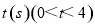 .
.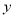 (cm2),求y与t之间的函数关系式;
(cm2),求y与t之间的函数关系式;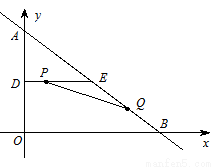
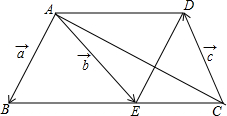 如图,在梯形ABCD中,AD∥BC,点E在边BC上,DE∥AB,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AE}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$.
如图,在梯形ABCD中,AD∥BC,点E在边BC上,DE∥AB,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AE}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$.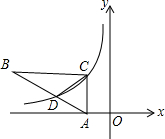 如图Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )
如图Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )