题目内容
4.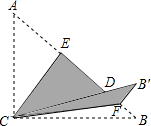 如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )| A. | $\frac{6}{5}$$\sqrt{10}$ | B. | 6 | C. | $\frac{8}{5}$$\sqrt{10}$ | D. | $\frac{24}{5}$ |
分析 首先根据折叠可得CD=AC=3,B′C=BC=4,∠ACE=∠DCE,∠BCF=∠B′CF,CE⊥AB,然后求得△ECF是等腰直角三角形,进而求得∠B′FD=90°,CE=EF=4.8,由勾股定理求出AE,得出BF,由勾股定理即可求得B′E的长.
解答 解:根据折叠的性质可知:DE=AE,∠ACE=∠DCE,∠BCF=∠B′CF,CE⊥AB,B′F=BF,
∴B′D=4-3=1,∠DCE+∠B′CF=∠ACE+∠BCF,
∵∠ACB=90°,
∴∠ECF=45°,
∴△ECF是等腰直角三角形,
∴EF=CE,∠EFC=45°,
∴∠BFC=∠B′FC=135°,
∴∠B′FE=90°,
∵S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CE,
∴AC•BC=AB•CE,
∵根据勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴CE=$\frac{AC•BC}{AB}$=4.8,
∴EF=4.8,AE=$\sqrt{A{C}^{2}-C{E}^{2}}$=3.6,
∴B′F=BF=AB-AE-EF=10-3.6-4.8=1.6,
∴B′E=$\sqrt{E{F}^{2}+B′{F}^{2}}$=$\sqrt{4.{8}^{2}+1.{6}^{2}}$=$\frac{8\sqrt{10}}{5}$.
故选:C.
点评 此题主要考查了翻折变换,等腰三角形的判定和性质,勾股定理等知识;熟练掌握翻折变换的性质,由直角三角形的性质和勾股定理求出CE、AE是解决问题的关键.

练习册系列答案
相关题目
9. 有理数a,b在数轴上对应点的位置如图所示,下列各式正确的是( )
有理数a,b在数轴上对应点的位置如图所示,下列各式正确的是( )
 有理数a,b在数轴上对应点的位置如图所示,下列各式正确的是( )
有理数a,b在数轴上对应点的位置如图所示,下列各式正确的是( )| A. | a+b<0 | B. | a-b<0 | C. | |a|>|b| | D. | $\frac{b}{a}>0$ |
16.若9x2-kx+4是一个完全平方式,则k的值是( )
| A. | 2 | B. | 6 | C. | 12 | D. | 12或-12 |
13.下列方程的变形,符合等式的性质的是( )
| A. | 由2x-3=7,得2x=7-3 | B. | 由3x-2=x+1,得3x-x=1-2 | ||
| C. | 由-2x=5,得x=-3 | D. | 由-$\frac{1}{3}$x=1,得x=-3 |
 如图,梯形ABCD中,AD∥BC,点E是边AD的中点,连结BE并延长交CD的延长线于点F,交AC于点G.
如图,梯形ABCD中,AD∥BC,点E是边AD的中点,连结BE并延长交CD的延长线于点F,交AC于点G.