题目内容
15. 如图,梯形ABCD中,AD∥BC,点E是边AD的中点,连结BE并延长交CD的延长线于点F,交AC于点G.
如图,梯形ABCD中,AD∥BC,点E是边AD的中点,连结BE并延长交CD的延长线于点F,交AC于点G.(1)若FD=2,$\frac{ED}{BC}=\frac{1}{3}$,求线段DC的长;
(2)求证:EF•GB=BF•GE.
分析 (1)由平行线得出△DEF∽△CBF,得出对应边成比例求出FC,即可得出DC的长;
(2)由平行线得出△DEF∽△CBF,△AEG∽△CBG,得出对应边成比例$\frac{EF}{BF}=\frac{DE}{BC}$,$\frac{AE}{BC}=\frac{GE}{GB}$,由已知条件得出AE=DE,因此$\frac{EF}{BF}=\frac{GE}{GB}$,即可得出结论.
解答 (1)解:∵AD∥BC,
∴△DEF∽△CBF,
∴$\frac{FD}{FC}=\frac{ED}{BC}$=$\frac{1}{3}$,
∴FC=3FD=6,
∴DC=FC-FD=4;
(2)证明:∵AD∥BC,
∴△DEF∽△CBF,△AEG∽△CBG,
∴$\frac{EF}{BF}=\frac{DE}{BC}$,$\frac{AE}{BC}=\frac{GE}{GB}$,
∵点E是边AD的中点,
∴AE=DE,
∴$\frac{EF}{BF}=\frac{GE}{GB}$,
∴EF•GB=BF•GE.
点评 本题考查了梯形的性质、相似三角形的判定与性质;熟练掌握梯形的性质,证明三角形相似得出比例式是解决问题的关键.

练习册系列答案
相关题目
7. 如图,根据a、b、c三个数表示在数轴上的情况,下列关系正确的是( )
如图,根据a、b、c三个数表示在数轴上的情况,下列关系正确的是( )
 如图,根据a、b、c三个数表示在数轴上的情况,下列关系正确的是( )
如图,根据a、b、c三个数表示在数轴上的情况,下列关系正确的是( )| A. | a<c | B. | a+b<0 | C. | |a|<|c| | D. | bc<0 |
4.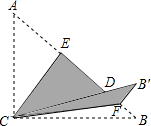 如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )
 如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )| A. | $\frac{6}{5}$$\sqrt{10}$ | B. | 6 | C. | $\frac{8}{5}$$\sqrt{10}$ | D. | $\frac{24}{5}$ |
5.-$\frac{1}{2}$的倒数是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
 如图,在△ABC中,AB=AC=10m,BC=16m,现点P从点B出发,沿BC向C点运动,运动速度为$\frac{1}{4}$m/s,若点P的运动时间为t秒,则当△ABP是直角三角形时,时间t的值为32s或50s.
如图,在△ABC中,AB=AC=10m,BC=16m,现点P从点B出发,沿BC向C点运动,运动速度为$\frac{1}{4}$m/s,若点P的运动时间为t秒,则当△ABP是直角三角形时,时间t的值为32s或50s.