题目内容
17.解下列方程:(1)5y-(8-3y)=3y+2(3y+5);
(2)$\frac{5-2y}{5}$-4=$\frac{y+2}{2}$-$\frac{4-7y}{10}$.
分析 (1)根据去括号、移项、合并同类项、系数化为1解答即可;
(2)根据去分母、去括号、移项、合并同类项、系数化为1解答即可.
解答 解:(1)5y-(8-3y)=3y+2(3y+5)
5y-8+3y=3y+6y+10
5y+3y-3y-6y=10+8
-y=18
y=-18;
(2)$\frac{5-2y}{5}$-4=$\frac{y+2}{2}$-$\frac{4-7y}{10}$
2(5-2y)-40=5(y+2)-(4-7y)
10-4y-40=5y+10-4+7y
-4y-5y-7y=10-4+40-10
-16y=36
y=-$\stackrel{\;}{\;}$$\frac{9}{4}$.
点评 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解.

练习册系列答案
相关题目
4.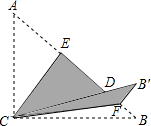 如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )
 如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )| A. | $\frac{6}{5}$$\sqrt{10}$ | B. | 6 | C. | $\frac{8}{5}$$\sqrt{10}$ | D. | $\frac{24}{5}$ |
 已知:如图:AB∥CD,AB=CD,AD、BC相交于点O,BE∥CF,BE、CF分别交AD于点E、F,
已知:如图:AB∥CD,AB=CD,AD、BC相交于点O,BE∥CF,BE、CF分别交AD于点E、F, 如图,在一个圆形时钟的表面上,OA表示时针,OB表示分针(O为两针的旋转中心).下午3点时,OA与OB成直角.
如图,在一个圆形时钟的表面上,OA表示时针,OB表示分针(O为两针的旋转中心).下午3点时,OA与OB成直角. 如图,在△ABC中,AB=AC=10m,BC=16m,现点P从点B出发,沿BC向C点运动,运动速度为$\frac{1}{4}$m/s,若点P的运动时间为t秒,则当△ABP是直角三角形时,时间t的值为32s或50s.
如图,在△ABC中,AB=AC=10m,BC=16m,现点P从点B出发,沿BC向C点运动,运动速度为$\frac{1}{4}$m/s,若点P的运动时间为t秒,则当△ABP是直角三角形时,时间t的值为32s或50s.