题目内容
19.如图,抛物线y=-x2+bx+c交x轴负半轴于点A,交X轴正半轴于点B,交y轴 正半轴于点C,直线BC的解析式为y=kx+3(k≠0 ),∠ABC=45°(1)求b、c的值;
(2)点P在第一象限的抛物线上,过点P分别作x轴、y轴的平行线,交直线BC于点M、N,设点P的横坐标为t,线段MN的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,点E为抛物线的顶点,连接EC、EP、AP,AP交y轴于点D,连接DM,若∠DMB=90°,求四边形CMPE的面积.

分析 (1)在y=kx+3中,令x=0,即可求得C的纵坐标,然后根据△OBC是等腰直角三角形求得B的坐标,利用待定系数法求得b和c的值;
(2)首先求得直线BC的解析式,则可求得P和N的纵坐标,则PN的长即可求得,然后根据△PMN是等腰直角三角形即可表示出MN的长;
(3)延长PM交y轴于点H,延长PN交x轴于点K,过E作EQ⊥y轴于点Q,连接EM,在直角△OAD和直角△KAP中,利用三角函数即可列方程求得t的值,再根据S四边形CMPE=S△ECM+S△EMP求解.
解答 解:(1)在y=kx+3中,令x=0,则y=3,即C的坐标是(0,3),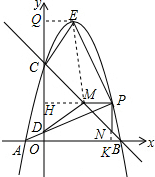
∵直角△OBC中,∠ABC=45°,
∴OB=OC=3,即B的坐标是(3,0).
根据题意得:$\left\{\begin{array}{l}{c=3}\\{-9+3b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{c=3}\\{b=2}\end{array}\right.$;
(2)二次函数的解析式是y=-x2+2x+3,
设BC的解析式是y=mx+n,
则$\left\{\begin{array}{l}{n=3}\\{3m+n=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-1}\\{n=3}\end{array}\right.$,
则直线BC的解析式是y=-x+3,△OBC是等腰直角三角形.
把x=t代入y=-x2+2x+3得y=-t2+2t+3,即P的纵坐标是-t2+2t+3,
把x=t代入y=-x+3,得y=-t+3,即Q的纵坐标是-t+3.
则PQ=(-t2+2t+3)-(-t+3)=-t2+3t,
则d=$\sqrt{2}$PQ,即d=-$\sqrt{2}$t2+3$\sqrt{2}$t;
(3)延长PM交y轴于点H,延长PN交x轴于点K.
A的坐标是(-1,0),P的坐标是(t,-t2+2t+3),
∵在直角△PAK中,tan∠PAK=$\frac{-{t}^{2}+2t+3}{t+1}$=3-t,
在直角△AOD中,∠DAO=$\frac{OD}{OA}$=$\frac{OD}{1}$,
∴3-t=$\frac{OD}{1}$,
∴OD=3-t,
∴CD=3-(3-t)=t.
∵△CMD是等腰直角三角形,
∴MH=$\frac{1}{2}$CD=$\frac{1}{2}$t.
∵PH=MH+PM,
∴t=$\frac{1}{2}$t+(-t2+3t).
∴t=$\frac{5}{2}$或0(舍去).
∴PM=-($\frac{5}{2}$)2+3×$\frac{5}{2}$=$\frac{5}{4}$,
PM=$\frac{5}{4}$,CM=$\frac{5\sqrt{2}}{4}$,PK=$\frac{7}{4}$.
∵二次函数的解析式是y=-x2+2x+3的顶点E的坐标是(1,4).
∴点E到PM的距离是4-$\frac{7}{4}$=$\frac{9}{4}$,
过E作EQ⊥y轴于点Q,连接EM.
∵EQ=QC=1,
∴△EQC和△HMC都是等腰直角三角形,
∴EC=$\sqrt{2}$,∠ECM=90°,
∴S四边形CMPE=S△ECM+S△EMP=$\frac{1}{2}$×$\sqrt{2}$×$\frac{5\sqrt{2}}{4}$+$\frac{1}{2}$×$\frac{5}{4}$×$\frac{9}{4}$=$\frac{85}{32}$.
点评 本题考查了待定系数法求函数的解析式以及图形的面积的计算,在(3)中正确求得t的值是解题的关键.

 如图,根据a、b、c三个数表示在数轴上的情况,下列关系正确的是( )
如图,根据a、b、c三个数表示在数轴上的情况,下列关系正确的是( )| A. | a<c | B. | a+b<0 | C. | |a|<|c| | D. | bc<0 |
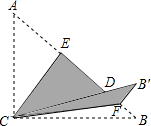 如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )| A. | $\frac{6}{5}$$\sqrt{10}$ | B. | 6 | C. | $\frac{8}{5}$$\sqrt{10}$ | D. | $\frac{24}{5}$ |
| A. | 1 | B. | 2 | C. | 4 | D. | 6 |
 如图,在一个圆形时钟的表面上,OA表示时针,OB表示分针(O为两针的旋转中心).下午3点时,OA与OB成直角.
如图,在一个圆形时钟的表面上,OA表示时针,OB表示分针(O为两针的旋转中心).下午3点时,OA与OB成直角.




