题目内容
12.已知抛物线y=2x2-bx+3的对称轴经过点(2,-1),则b的值为8.分析 根据公式法可求对称轴,可得关于b的一元一次方程,解方程即可.
解答 解:∵抛物线y=2x2-bx+3的对称轴经过点(2,-1),
∴对称轴x=-$\frac{-b}{2×2}$=2,
解得:b=8.
故答案为8.
点评 此题考查二次函数的性质,掌握利用公式法求对称轴是解决问题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
7. 如图,根据a、b、c三个数表示在数轴上的情况,下列关系正确的是( )
如图,根据a、b、c三个数表示在数轴上的情况,下列关系正确的是( )
 如图,根据a、b、c三个数表示在数轴上的情况,下列关系正确的是( )
如图,根据a、b、c三个数表示在数轴上的情况,下列关系正确的是( )| A. | a<c | B. | a+b<0 | C. | |a|<|c| | D. | bc<0 |
4.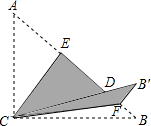 如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )
 如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )| A. | $\frac{6}{5}$$\sqrt{10}$ | B. | 6 | C. | $\frac{8}{5}$$\sqrt{10}$ | D. | $\frac{24}{5}$ |
2.单项式-32xy2z3的系数和次数分别是( )
| A. | -1,8 | B. | -3,8 | C. | -9,6 | D. | -9,3 |
 已知:如图:AB∥CD,AB=CD,AD、BC相交于点O,BE∥CF,BE、CF分别交AD于点E、F,
已知:如图:AB∥CD,AB=CD,AD、BC相交于点O,BE∥CF,BE、CF分别交AD于点E、F, 我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等,但是当这两个三角形均为直角三角形,或均为钝角三角形,或均为锐角三角形时它们全等.
我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等,但是当这两个三角形均为直角三角形,或均为钝角三角形,或均为锐角三角形时它们全等. 如图,已知:在△ABC中,AB=AC.
如图,已知:在△ABC中,AB=AC.