题目内容
20．
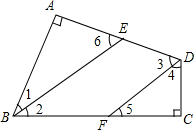如图，在四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，BE∥DF，求证：DF平分∠ADC．
分析 先根据角平分线的性质得出∠1=∠2，再由平行线的性质得出∠2=∠5，∠3=∠6，故可得出∠1=∠5，由∠A=∠C=90°可知∠1+∠6=90°，∠4+∠5=90°，故可得出∠4=∠6，由此可得出结论．
解答 证明：∵BE平分∠ABC，
∴∠1=∠2．
∵BE∥DF，
∴∠2=∠5，∠3=∠6，
∴∠1=∠5．
∵∠A=∠C=90°，
∴∠1+∠6=90°，∠4+∠5=90°，
∴∠4=∠6，
∴∠3=∠4，即DF平分∠ADC．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
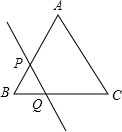如图，在正△ABC中，AB=10cm，直线PQ由点B出发，沿BA的方向匀速运动，速度为1cm/s，运动时间为t（s）（0＜t＜5），则BP=$\frac{2\sqrt{3}}{3}t$．（用t的代数式表示）
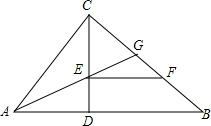如图，△ABC中，∠ACB=90°，CD是高，AG平分∠CAB，EF∥AB，AC=6，BC=8．