题目内容
11.当x为何值时,下列分式有意义?(1)$\frac{1}{4x}$;
(2)$\frac{3x+1}{3-7x}$;
(3)$\frac{x+1}{{(2x+1)}^{2}}$;
(4)$\frac{1}{(x-1)(2x+4)}$.
分析 分式有意义的条件是分母不等于零.
解答 解:(1)∵分式$\frac{1}{4x}$有意义,
∴4x≠0.
∴x≠0;
(2)∵$\frac{3x+1}{3-7x}$有意义,
∴3-7x≠0.
解得:x≠$\frac{7}{3}$;
(3)∵分式$\frac{x+1}{{(2x+1)}^{2}}$有意义,
∴2x+1≠0.
解得:x≠-$\frac{1}{2}$;
(4)∵分式$\frac{1}{(x-1)(2x+4)}$有意义,
∴(x-1)(2x+4)≠0.
解得:x1≠1,x2≠-2.
点评 本题主要考查的是分式有意义的条件,掌握分式有意义的条件是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.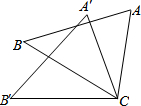 如图,△ACB≌△A′C′B′,∠A=40°,则∠A′的度数为( )
如图,△ACB≌△A′C′B′,∠A=40°,则∠A′的度数为( )
 如图,△ACB≌△A′C′B′,∠A=40°,则∠A′的度数为( )
如图,△ACB≌△A′C′B′,∠A=40°,则∠A′的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
8. 如图,在梯形ABCD中,AB∥CD,∠ADC=90度,AB=AD=2,E是AD边上一点(点E不与A,D重合),BE的垂直平分线交边AB于M,交直线CD于N.设四边形ADNM的面积为S,则S的最大值是( )
如图,在梯形ABCD中,AB∥CD,∠ADC=90度,AB=AD=2,E是AD边上一点(点E不与A,D重合),BE的垂直平分线交边AB于M,交直线CD于N.设四边形ADNM的面积为S,则S的最大值是( )
 如图,在梯形ABCD中,AB∥CD,∠ADC=90度,AB=AD=2,E是AD边上一点(点E不与A,D重合),BE的垂直平分线交边AB于M,交直线CD于N.设四边形ADNM的面积为S,则S的最大值是( )
如图,在梯形ABCD中,AB∥CD,∠ADC=90度,AB=AD=2,E是AD边上一点(点E不与A,D重合),BE的垂直平分线交边AB于M,交直线CD于N.设四边形ADNM的面积为S,则S的最大值是( )| A. | $\frac{5}{3}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{5}{2}$ |
 按如图所示的程序计算,若开始输入的x的值为48,我们发现第一次得到的结果为24,第二次得到的结果为12,…,则第2016次得到的结果为-1.
按如图所示的程序计算,若开始输入的x的值为48,我们发现第一次得到的结果为24,第二次得到的结果为12,…,则第2016次得到的结果为-1. 如图,在直角坐标系中,经过点A(2,6)、点B(10,2)的直线与两条坐标轴分别相交于C、D两点,点P是x轴上的一点
如图,在直角坐标系中,经过点A(2,6)、点B(10,2)的直线与两条坐标轴分别相交于C、D两点,点P是x轴上的一点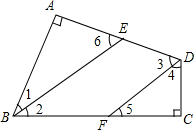 如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,BE∥DF,求证:DF平分∠ADC.
如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,BE∥DF,求证:DF平分∠ADC.