题目内容
8.若y=$\sqrt{4x-3}$+$\sqrt{3-4x}$-5,则x=$\frac{3}{4}$,y=-5.分析 先根据二次根式的基本性质:$\sqrt{a}$有意义,则a≥0求出x的值,再代入计算即可求解.
解答 解:∵y=$\sqrt{4x-3}$+$\sqrt{3-4x}$-5,
∴4x-3≥0,则有x≥$\frac{3}{4}$;3-4x≥0,则有x≤$\frac{3}{4}$,综合得x=$\frac{3}{4}$,
将x=$\frac{3}{4}$代入y=$\sqrt{4x-3}$+$\sqrt{3-4x}$-5,得y=0+0-5=-5.
故答案为:$\frac{3}{4}$,-5.
点评 考查了二次根式有意义的条件,解决此题的关键:掌握二次根式的基本性质:$\sqrt{a}$有意义,则a≥0.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 如图,在直角坐标系中,经过点A(2,6)、点B(10,2)的直线与两条坐标轴分别相交于C、D两点,点P是x轴上的一点
如图,在直角坐标系中,经过点A(2,6)、点B(10,2)的直线与两条坐标轴分别相交于C、D两点,点P是x轴上的一点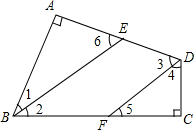 如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,BE∥DF,求证:DF平分∠ADC.
如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,BE∥DF,求证:DF平分∠ADC. 如图,Rt△ACB中,AC=BC,∠ACB=90°,D、E为AB上两点,且∠DCE=45°,F为△ABC外一点,且FB⊥AB,FC⊥CD,则下列结论:
如图,Rt△ACB中,AC=BC,∠ACB=90°,D、E为AB上两点,且∠DCE=45°,F为△ABC外一点,且FB⊥AB,FC⊥CD,则下列结论: