题目内容
10.某商场要经营一种新上市的文具,进价为60元/件.试营销阶段发现:当销售单价是70元时,每天的销售量为40件;现以每5元的方式涨价(即涨价数必为5元的整数倍),销售单价每上涨5元,每天的销售量就减少3件.(1)直接写出商场销售这种文具,每天的销售量y(件)与销售单价x(元)之间的函数关系式:y=$-\frac{3x}{5}+82$.
(2)求出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;求销售单价为多少元时,该文具每天的销售利润最大;
(3)若商场要求销售量不低于16件,要想文具每天的销售利润为680元,那么销售单价应该定为多少元?
分析 (1)根据题意可以得到每天的销售量y(件)与销售单价x(元)之间的函数关系式;
(2)根据题意可以得到每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式,然后将函数关系式化为顶点式,注意涨价数为5元的整数倍,即可求得销售单价为多少元时,该文具每天的销售利润最大;
(3)根据商场要求销售量不低于16件,要想文具每天的销售利润为680元,可以求得销售单价应该定为多少元,本题得以解决.
解答 解:(1)由题意可得,
每天的销售量y(件)与销售单价x(元)之间的函数关系式是:y=40-$\frac{x-70}{5}×3$=$-\frac{3x}{5}+82$,
即每天的销售量y(件)与销售单价x(元)之间的函数关系式是:y=$-\frac{3x}{5}+82$;
(2)由题意可得,
w=(x-60)×$(-\frac{3x}{5}+82)$=$-\frac{3{x}^{2}}{5}+118x-4920$=$-\frac{3}{5}(x-\frac{295}{3})^{2}+\frac{2645}{3}$,
∴当x=$\frac{295}{3}$=$98\frac{1}{3}$,w取得最大值,
∵涨价数为5元的整数倍,
∴x=95时,w=875;x=100时,w=880;
即每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式是:w=$-\frac{3}{5}(x-\frac{295}{3})^{2}+\frac{2645}{3}$,销售单价为100元时,该文具每天的销售利润最大;
(3)由题意可得,
$y=-\frac{3x}{5}+82≥16$,
解得,x≤110,
w=$-\frac{3}{5}(x-\frac{295}{3})^{2}+\frac{2645}{3}$=680,
解得,${x}_{1}=80,{x}_{2}=\frac{350}{3}=116\frac{2}{3}$(舍去),
即若商场要求销售量不低于16件,要想文具每天的销售利润为680元,那么销售单价应该定为80元.
点评 本题考查二次函数的应用,求函数的解析式、求二次函数的最值,解题的关键是明确题意,列出相应的函数关系式,会将函数解析式化为顶点式,会求函数的最值,需要注意的是涨价数为5元的整数倍.

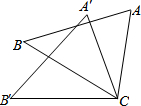 如图,△ACB≌△A′C′B′,∠A=40°,则∠A′的度数为( )
如图,△ACB≌△A′C′B′,∠A=40°,则∠A′的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
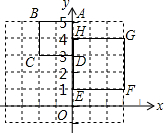 如图,正方形ABCD与正方形EFGH是位似形,已知A(0,5),D(0,3),E(0,1),H(0,4),则位似中心的坐标是(0,$\frac{17}{5}$),(-6,7).
如图,正方形ABCD与正方形EFGH是位似形,已知A(0,5),D(0,3),E(0,1),H(0,4),则位似中心的坐标是(0,$\frac{17}{5}$),(-6,7). 按如图所示的程序计算,若开始输入的x的值为48,我们发现第一次得到的结果为24,第二次得到的结果为12,…,则第2016次得到的结果为-1.
按如图所示的程序计算,若开始输入的x的值为48,我们发现第一次得到的结果为24,第二次得到的结果为12,…,则第2016次得到的结果为-1. 如图,矩形ABCD中,对角线AC,BD交于点O,DE⊥AC于点E,若BC=6,∠BOC=120°,求DE的长.
如图,矩形ABCD中,对角线AC,BD交于点O,DE⊥AC于点E,若BC=6,∠BOC=120°,求DE的长. 如图,在直角坐标系中,经过点A(2,6)、点B(10,2)的直线与两条坐标轴分别相交于C、D两点,点P是x轴上的一点
如图,在直角坐标系中,经过点A(2,6)、点B(10,2)的直线与两条坐标轴分别相交于C、D两点,点P是x轴上的一点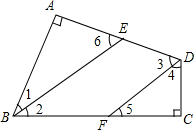 如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,BE∥DF,求证:DF平分∠ADC.
如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,BE∥DF,求证:DF平分∠ADC.