题目内容
9.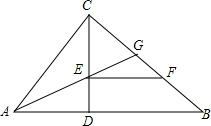 如图,△ABC中,∠ACB=90°,CD是高,AG平分∠CAB,EF∥AB,AC=6,BC=8.
如图,△ABC中,∠ACB=90°,CD是高,AG平分∠CAB,EF∥AB,AC=6,BC=8.(1)求证:CE=FB;
(2)求FG的长.
分析 (1)先证CE=CG,从而将问题转化为证CG=BF,由于CG与BF之间为线段GF,从而只需证明CF=BF即可,于是作GH⊥AB于H,证明△CEF≌△GHB即可得出结论;
(2)先算出AB的长,再利用角平分线比例定理直接算出CG和BG的长度,结合(1)中结论即可算出FG的长.
解答 解:(1)∵AG平分∠CAB,
∴∠CAG=∠BAG,
∵∠ACG=90°,
∴∠CAG+∠CGA=90°,
∵CD⊥AB,
∴∠DAE+∠DEA=90°,
∵∠DEA=∠CEG,
∴∠CEG=∠CGE,
∴CE=CG,
作GH⊥AB于H,如图,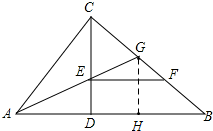
则GH=GC=CE,
∵EF∥AB,
∴EF⊥CD,∠CFE=∠GBH,
在△CEF和△GHB中,
$\left\{\begin{array}{l}{∠CEF=∠GHB}\\{CE=GH}\\{∠CFE=∠GBH}\end{array}\right.$,
∴△CEF≌△GHB(AAS),
∴CF=BG,
∴BF=CG=CE;
(2)∵AC=6,BC=8,
∴AB=10,
∵AG平分∠CAB,
∴$\frac{AC}{AB}=\frac{CG}{GB}$,
∴$\frac{CG}{GB}=\frac{6}{10}=\frac{3}{5}$,
∴$CG=\frac{3}{8}BC=3$,
∴GB=5,
∴GF=GB-BF=5-3=2.
点评 本题主要考查了角平分线的性质、全等三角形的判定与性质、勾股定理、角平分线比例定理,难度中等.(1)中CE=CG是基本结论,可记住,以后遇到类似情景可迅速反应;(2)问利用角平分线比例定理算线段长度非常方便,要特别注意一下.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
8. 如图,在梯形ABCD中,AB∥CD,∠ADC=90度,AB=AD=2,E是AD边上一点(点E不与A,D重合),BE的垂直平分线交边AB于M,交直线CD于N.设四边形ADNM的面积为S,则S的最大值是( )
如图,在梯形ABCD中,AB∥CD,∠ADC=90度,AB=AD=2,E是AD边上一点(点E不与A,D重合),BE的垂直平分线交边AB于M,交直线CD于N.设四边形ADNM的面积为S,则S的最大值是( )
 如图,在梯形ABCD中,AB∥CD,∠ADC=90度,AB=AD=2,E是AD边上一点(点E不与A,D重合),BE的垂直平分线交边AB于M,交直线CD于N.设四边形ADNM的面积为S,则S的最大值是( )
如图,在梯形ABCD中,AB∥CD,∠ADC=90度,AB=AD=2,E是AD边上一点(点E不与A,D重合),BE的垂直平分线交边AB于M,交直线CD于N.设四边形ADNM的面积为S,则S的最大值是( )| A. | $\frac{5}{3}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{5}{2}$ |
 如图,在直角坐标系中,经过点A(2,6)、点B(10,2)的直线与两条坐标轴分别相交于C、D两点,点P是x轴上的一点
如图,在直角坐标系中,经过点A(2,6)、点B(10,2)的直线与两条坐标轴分别相交于C、D两点,点P是x轴上的一点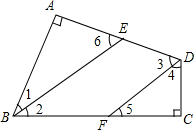 如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,BE∥DF,求证:DF平分∠ADC.
如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,BE∥DF,求证:DF平分∠ADC. 如图,在⊙O中,P为$\widehat{BAC}$的中点,PD⊥CD,CD交⊙O于A,若AC=3,AD=2,则AB的长为7.
如图,在⊙O中,P为$\widehat{BAC}$的中点,PD⊥CD,CD交⊙O于A,若AC=3,AD=2,则AB的长为7. 如图,Rt△ACB中,AC=BC,∠ACB=90°,D、E为AB上两点,且∠DCE=45°,F为△ABC外一点,且FB⊥AB,FC⊥CD,则下列结论:
如图,Rt△ACB中,AC=BC,∠ACB=90°,D、E为AB上两点,且∠DCE=45°,F为△ABC外一点,且FB⊥AB,FC⊥CD,则下列结论: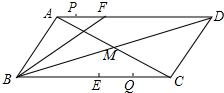 如图,在平行四边形ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动.点P运动到F点时停止运动,点Q也同时停止运动.当点P运动3或5秒时,以点P、Q、E、F为顶点的四边形是平行四边形.
如图,在平行四边形ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动.点P运动到F点时停止运动,点Q也同时停止运动.当点P运动3或5秒时,以点P、Q、E、F为顶点的四边形是平行四边形.