题目内容
 如图,抛物线y=
如图,抛物线y=| 1 |
| 4 |
(1)求该抛物线的解析式;
(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
考点:二次函数综合题,勾股定理,平行四边形的判定,相似三角形的应用
专题:代数几何综合题,压轴题
分析:(1)利用待定系数法求出抛物线的解析式;
(2)首先求出对称点A′的坐标,然后代入抛物线解析式,即可判定点A′是否在抛物线上.本问关键在于求出A′的坐标.如答图所示,作辅助线,构造一对相似三角形Rt△A′EA∽Rt△OAC,利用相似关系、对称性质、勾股定理,求出对称点A′的坐标;
(3)本问为存在型问题.解题要点是利用平行四边形的定义,列出代数关系式求解.如答图所示,平行四边形的对边平行且相等,因此PM=AC=10;利用含未知数的代数式表示出PM的长度,然后列方程求解.
(2)首先求出对称点A′的坐标,然后代入抛物线解析式,即可判定点A′是否在抛物线上.本问关键在于求出A′的坐标.如答图所示,作辅助线,构造一对相似三角形Rt△A′EA∽Rt△OAC,利用相似关系、对称性质、勾股定理,求出对称点A′的坐标;
(3)本问为存在型问题.解题要点是利用平行四边形的定义,列出代数关系式求解.如答图所示,平行四边形的对边平行且相等,因此PM=AC=10;利用含未知数的代数式表示出PM的长度,然后列方程求解.
解答: 解:(1)∵y=
解:(1)∵y=
x2+bx+c与x轴交于A(5,0)、B(-1,0)两点,
∴
,
解得
.
∴抛物线的解析式为y=
x2-x-
.
(2)如答图所示,过点A′作A′E⊥x轴于E,AA′与OC交于点D,
∵点C在直线y=2x上,
∴C(5,10)
∵点A和A′关于直线y=2x对称,
∴OC⊥AA′,A′D=AD.
∵OA=5,AC=10,
∴OC=
=
=5
.
∵S△OAC=
OC•AD=
OA•AC,
∴AD=2
.
∴AA′=4
,
在Rt△A′EA和Rt△OAC中,
∵∠A′AE+∠A′AC=90°,
∠ACD+∠A′AC=90°,
∴∠A′AE=∠ACD.
又∵∠A′EA=∠OAC=90°,
∴Rt△A′EA∽Rt△OAC.
∴
=
=
,
即
=
=
.
∴A′E=4,AE=8.
∴OE=AE-OA=3.
∴点A′的坐标为(-3,4),
当x=-3时,
y=
×(-3)2+3-
=4.
所以,点A′在该抛物线上.
(3)存在.
理由:设直线CA′的解析式为y=kx+b,
则
,
解得
∴直线CA′的解析式为y=
x+
设点P的坐标为(x,
x2-x-
),则点M为(x,
x+
).
∵PM∥AC,
∴要使四边形PACM是平行四边形,只需PM=AC.又点M在点P的上方,
∴(
x+
)-(
x2-x-
)=10.
解得x1=2,x2=5(不合题意,舍去)
当x=2时,y=-
.
∴当点P运动到(2,-
)时,四边形PACM是平行四边形.
 解:(1)∵y=
解:(1)∵y=| 1 |
| 4 |
∴
|
解得
|
∴抛物线的解析式为y=
| 1 |
| 4 |
| 5 |
| 4 |
(2)如答图所示,过点A′作A′E⊥x轴于E,AA′与OC交于点D,
∵点C在直线y=2x上,
∴C(5,10)
∵点A和A′关于直线y=2x对称,
∴OC⊥AA′,A′D=AD.
∵OA=5,AC=10,
∴OC=
| OA2+AC2 |
| 52+102 |
| 5 |
∵S△OAC=
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=2
| 5 |
∴AA′=4
| 5 |
在Rt△A′EA和Rt△OAC中,
∵∠A′AE+∠A′AC=90°,
∠ACD+∠A′AC=90°,
∴∠A′AE=∠ACD.
又∵∠A′EA=∠OAC=90°,
∴Rt△A′EA∽Rt△OAC.
∴
| A′E |
| OA |
| AE |
| AC |
| AA′ |
| OC |
即
| A′E |
| 5 |
| AE |
| 10 |
4
| ||
5
|
∴A′E=4,AE=8.
∴OE=AE-OA=3.
∴点A′的坐标为(-3,4),
当x=-3时,
y=
| 1 |
| 4 |
| 5 |
| 4 |
所以,点A′在该抛物线上.
(3)存在.
理由:设直线CA′的解析式为y=kx+b,
则
|
解得
|
∴直线CA′的解析式为y=
| 3 |
| 4 |
| 25 |
| 4 |
设点P的坐标为(x,
| 1 |
| 4 |
| 5 |
| 4 |
| 3 |
| 4 |
| 25 |
| 4 |
∵PM∥AC,
∴要使四边形PACM是平行四边形,只需PM=AC.又点M在点P的上方,
∴(
| 3 |
| 4 |
| 25 |
| 4 |
| 1 |
| 4 |
| 5 |
| 4 |
解得x1=2,x2=5(不合题意,舍去)
当x=2时,y=-
| 9 |
| 4 |
∴当点P运动到(2,-
| 9 |
| 4 |
点评:本题是二次函数的综合题型,考查了二次函数的图象及性质、待定系数法、相似、平行四边形、勾股定理、对称等知识点,涉及考点较多,有一定的难度.第(2)问的要点是求对称点A′的坐标,第(3)问的要点是利用平行四边形的定义列方程求解.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
已知x-y=7,xy=2,则x2+y2的值为( )
| A、53 | B、45 | C、47 | D、51 |

 如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.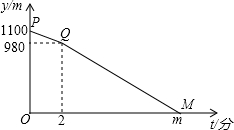 A,B两地相距1100米,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2分钟,乙出发7分钟后与甲相遇.设甲、乙两人相距y米,甲行进的时间为t分钟,y与t之间的函数关系如图所示.请你结合图象探究:
A,B两地相距1100米,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2分钟,乙出发7分钟后与甲相遇.设甲、乙两人相距y米,甲行进的时间为t分钟,y与t之间的函数关系如图所示.请你结合图象探究: