题目内容
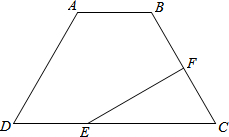已知：如图，梯形ABCD中，AD=BC，F为BC的中点，AB=2，∠A=120°，过点F作EF⊥BC交DC于点E，且EF=3，求DC的长．考点：梯形
专题：
分析：先求出△BEC是等边三角形，可求出EC=2CF=
EF=2
，再证出四边形ABCD是平行四边形，求出DE=AB=2，就可求出DC．
2
| ||
| 3 |
| 3 |
解答：解：如图连结BE，
∵梯形ABCD是等腰梯形，且∠A=120°，
∴∠D=∠C=180°-120°=60°，
又∵EF⊥BC，F为BC的中点，
∴EC=EB
∴△BEC是等边三角形，
∴在RT△EFC中，∠CEF=30°，EF=3，
∴EC=2CF=
EF=2
，
∵∠D=∠BEC=60°，
∴AD∥EB，
又∵AB∥DE，
∴四边形ABCD是平行四边形，
∴DE=AB=2，
∴DC=DC+EC=2
+2．
∵梯形ABCD是等腰梯形，且∠A=120°，
∴∠D=∠C=180°-120°=60°，
又∵EF⊥BC，F为BC的中点，
∴EC=EB
∴△BEC是等边三角形，
∴在RT△EFC中，∠CEF=30°，EF=3，
∴EC=2CF=
2
| ||
| 3 |
| 3 |
∵∠D=∠BEC=60°，
∴AD∥EB，
又∵AB∥DE，
∴四边形ABCD是平行四边形，
∴DE=AB=2，
∴DC=DC+EC=2
| 3 |
点评：本题主要考查等腰梯形的性质及平行四边形的判定，解此题的关键是用中垂线的性质证出△BEC是等边三角形．
练习册系列答案
相关题目
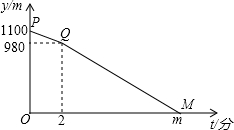A，B两地相距1100米，甲从A地出发，乙从B地出发，相向而行，甲比乙先出发2分钟，乙出发7分钟后与甲相遇．设甲、乙两人相距y米，甲行进的时间为t分钟，y与t之间的函数关系如图所示．请你结合图象探究：
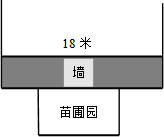大陇初级中学课外活动小组准备围建一个矩形生物苗圃园，其中一边靠墙，另外三边用长为30米的篱笆围成．如图已知墙长为18米，设这个苗圃园垂直于墙的一边的长为x米．
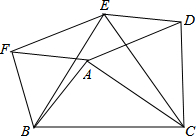已知，如图，△ABF，△ACD，△BCE都是等边三角形，求证：四边形ADEF是平行四边形．
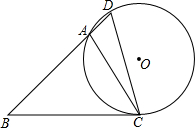如图，在△ABC中，∠B=45°，∠ACB=60°，AB=3