题目内容
在数学课上，同学们研究图形的拼接问题．
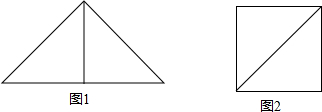
比如：两个全等的等腰直角三角形纸片既能拼成一个大的等腰直角三角形（如图1），也能拼成一个正方形（如图2）．
（1）现有两个相似的直角三角形纸片，各有一个角为30°，恰好可以拼成另一个含有30°角的直角三角形，那么在原来的两个三角形纸片中，较大的与较小的纸片的相似比为 ，请画出拼接的示意图；
（2）现有一个矩形恰好由三个各有一个角为30°的直角三角形纸片拼成，请你画出两种不同拼法的示意图．在拼成这个矩形的三角形中，若每种拼法中最小的三角形的斜边长为a，请直接写出每种拼法中最大三角形的斜边长．
比如：两个全等的等腰直角三角形纸片既能拼成一个大的等腰直角三角形（如图1），也能拼成一个正方形（如图2）．
（1）现有两个相似的直角三角形纸片，各有一个角为30°，恰好可以拼成另一个含有30°角的直角三角形，那么在原来的两个三角形纸片中，较大的与较小的纸片的相似比为
（2）现有一个矩形恰好由三个各有一个角为30°的直角三角形纸片拼成，请你画出两种不同拼法的示意图．在拼成这个矩形的三角形中，若每种拼法中最小的三角形的斜边长为a，请直接写出每种拼法中最大三角形的斜边长．
考点：图形的剪拼
专题：
分析：（1）利用相似三角形的性质当一组对应边相等，进而得出符合题意的图形即可；
（2）利用在直角三角形中30°所对的边等于斜边的一半进而求出即可．
（2）利用在直角三角形中30°所对的边等于斜边的一半进而求出即可．
解答：
解：（1）如图所示：较大的与较小的纸片的相似比为：tan60°=
：1，
故答案为：
：1；
（2）如图所示：
最大三角形的斜边长分别是2a，2a．
解：（1）如图所示：较大的与较小的纸片的相似比为：tan60°=| 3 |
故答案为：
| 3 |
（2）如图所示：
最大三角形的斜边长分别是2a，2a．
点评：此题主要考查了图形的剪拼以及直角三角形中30°所对的边等于斜边的一半的知识，得出边角关系是解题关键．
练习册系列答案
相关题目
如图，四边形ABCD是平行四边形，点N是AB上一点，且BN=2AN，AC、DN相交于点M，则S△ADM：S四边形CMNB的值为（ ）| A、3：11 | B、1：3 |
| C、1：9 | D、3：10 |
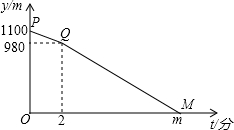A，B两地相距1100米，甲从A地出发，乙从B地出发，相向而行，甲比乙先出发2分钟，乙出发7分钟后与甲相遇．设甲、乙两人相距y米，甲行进的时间为t分钟，y与t之间的函数关系如图所示．请你结合图象探究：
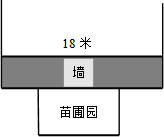大陇初级中学课外活动小组准备围建一个矩形生物苗圃园，其中一边靠墙，另外三边用长为30米的篱笆围成．如图已知墙长为18米，设这个苗圃园垂直于墙的一边的长为x米．