题目内容
19．
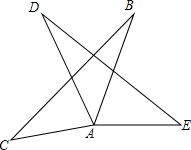如图，已知△ADE≌△ABC，∠DAE=110°，∠D=20°，求∠C的度数．
分析 先利用全等三角形的性质得∠BAC=∠DAE=110°，∠B=∠D=20°，然后根据三角形内角和计算∠C的度数．
解答 解：∵△ADE≌△ABC，
∴∠BAC=∠DAE=110°，∠B=∠D=20°，
∵∠C+∠BAC+∠B=180°，
∴∠C=180°-110°-20°=50°．
点评 本题考查了全等三角形的性质：全等三角形的对应边相等，全等三角形的对应角相等；全等三角形的性质是证明线段和角相等的理论依据，应用时要会找对应角和对应边．
练习册系列答案
名校课堂系列答案
相关题目
10．若字母A表示算式：$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$，则式子（1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$）（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{6}$）-（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$）×（1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{6}$）用含A的代数式表示为（ ）
| A． | （1+A）（A+$\frac{1}{6}$）-A（A+$\frac{1}{6}$） | B． | （1+A）（A+$\frac{1}{6}$）-A（A-$\frac{1}{6}$） | C． | （1+A）（A+$\frac{1}{6}$）-A（1+A） | D． | （1+A）（A+$\frac{1}{6}$）-A（A+$\frac{7}{6}$） |
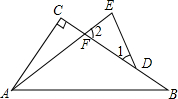如图，在△ABC中，∠C=90°，F、D是BC上两点，E是AF延长线上一点，∠B=∠1，∠E=∠2，BF=kDE．试探究AB、BC、DE之间的数量关系．（用含有k的代数式表示）