题目内容
14.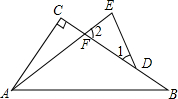 如图,在△ABC中,∠C=90°,F、D是BC上两点,E是AF延长线上一点,∠B=∠1,∠E=∠2,BF=kDE.试探究AB、BC、DE之间的数量关系.(用含有k的代数式表示)
如图,在△ABC中,∠C=90°,F、D是BC上两点,E是AF延长线上一点,∠B=∠1,∠E=∠2,BF=kDE.试探究AB、BC、DE之间的数量关系.(用含有k的代数式表示)
分析 延长BC到G,使BG=AB,由∠B=∠1,∠2=∠E,得到DE=DF,$\frac{DE}{DF}=\frac{BG}{AB}$=1,推出△DEF∽△BAG,于是得到∠G=∠2=∠CFA,证得△GAF是等腰三角形,根据等腰三角形的性质得到CG=CF,设ED=x,则FD=x,FB=kxBC=kx=CF,①,由于GC=CF=GB-BC,②,于是得到BC-kx=GB-BC,即可得到结论.
解答  证明:延长BC到G,使BG=AB,
证明:延长BC到G,使BG=AB,
∵∠B=∠1,∠2=∠E,
∴DE=DF,
∴$\frac{DE}{DF}=\frac{BG}{AB}$=1,
∴△DEF∽△BAG,
∴∠G=∠2=∠CFA,
∴△GAF是等腰三角形,
∵AG⊥GF,
∴CG=CF,
∵AB=GB,GB=GC=BC,
设ED=x,则FD=x,FB=kxBC=kx=CF,
∵GC=CF=GB-BC,
∴BC-kx=GB-BC,
∵GB=AB,
∴2BC=kDE=AB.
点评 本题考查了相似三角形的判定和性质,等腰三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
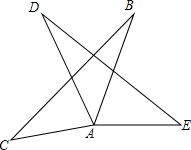 如图,已知△ADE≌△ABC,∠DAE=110°,∠D=20°,求∠C的度数.
如图,已知△ADE≌△ABC,∠DAE=110°,∠D=20°,求∠C的度数.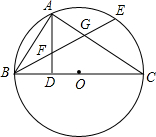 如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,$\widehat{AE}$=$\widehat{AB}$,BE分别交AD、AC于点F、G,判断△FAG的形状,并说明理由.
如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,$\widehat{AE}$=$\widehat{AB}$,BE分别交AD、AC于点F、G,判断△FAG的形状,并说明理由.