题目内容
1．写出二次项系数为5，以x1=1，x2=2为根的一元二次方程5x2-15x+10=0．分析 先计算出1+2和1×2，则根据根与系数的关系写出二次项系数为1的一元二方程，然后把两方程两边乘以5即可得到满足条件的方程．
解答 解：∵1+2=3，1×2=2，
∴以x1=1，x2=2为根的一元二次方程可为x2-3x+2=0，
当二次项系数为5，方程为5x2-15x+10=0．
故答案为5x2-15x+10=0．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
相关题目
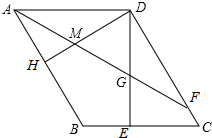如图，已知平行四边形ABCD中，DE⊥BC于点E，DH⊥AB于点H，AF平分∠BAD，分别交DC、DE、DH于点F、G、M，且DE=AD，CE=3，AB=5．
如图，在△ABC中，AB的垂直平分线分别交AB，AC于D，E两点，若AC=9cm，BC=5cm，则△BCE的周长为14cm．
13．
已知如图，△ABC中，AB=AC，AB的垂直平分线交AC于D，△ABC和△DBC的周长分别是60cm和38cm，则△ABC的腰和底边长分别为（ ）
已知如图，△ABC中，AB=AC，AB的垂直平分线交AC于D，△ABC和△DBC的周长分别是60cm和38cm，则△ABC的腰和底边长分别为（ ）| A． | 24cm和12cm | B． | 16cm和22cm | C． | 20cm和16cm | D． | 22cm和16cm |
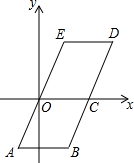如图，四边形ABCO和OCDE是两个形状相同，大小相等的平行四边形，已知点A（-1，-2），D（4，2），求点B、C、E的坐标及平行四边形ABDE的面积．
已知二次函数y=x2+mx+n的图象经过点A（1，0）和D（4，3），与x轴的另一个交点为B，与y轴交于点C．