题目内容
9.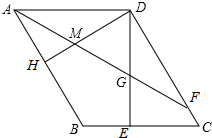 如图,已知平行四边形ABCD中,DE⊥BC于点E,DH⊥AB于点H,AF平分∠BAD,分别交DC、DE、DH于点F、G、M,且DE=AD,CE=3,AB=5.
如图,已知平行四边形ABCD中,DE⊥BC于点E,DH⊥AB于点H,AF平分∠BAD,分别交DC、DE、DH于点F、G、M,且DE=AD,CE=3,AB=5.(1)求线段CF的长度;
(2)求证:AB=DG+CE.
分析 (1)利用平行四边形的性质结合勾股定理得出DE的长,进而得出答案;
(2)利用全等三角形的判定方法得出△ADG≌△FDM(ASA),进而得出△AND≌△ECD(ASA),求出ND=MN+DM=EC+DG=AB.
解答  解:(1)如图1,∵四边形ABCD是平行四边形,
解:(1)如图1,∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠BAF=∠DFA,
∵∠DAF=∠BAF,
∴∠DAF=∠DFA,
∴AD=DF,
∵CE=3,AB=5,DE⊥BC于点E,
∴DC=5,
∴DE=AD=4,
∴DF=4,
∴FC=1;
(2)证明:如图2,过点A作AD的垂线交DH的延长线于点N,
∵DH⊥AB,AB∥DC,
∴∠HDF=90°,
在△ADG和△FDM中
∵$\left\{\begin{array}{l}{∠DAF=∠DFM}\\{AD=DF}\\{∠ADG=∠MDF}\end{array}\right.$,
∴△ADG≌△FDM(ASA),
∴DM=DG,∠5=∠4,
∵AN∥DE,
∴∠NAM=∠4,
∴∠NAM=∠6=∠5=∠4,
∴AN=MN,
∵∠1+∠3=90°,∠2+∠3=90°,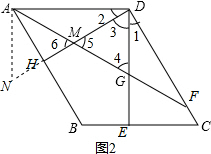
∴∠1=∠2,
在△AND和△ECD中
∵$\left\{\begin{array}{l}{∠2=∠1}\\{AD=DE}\\{∠DAN=∠DEC}\end{array}\right.$,
∴△AND≌△ECD(AAS),
∴AN=EC,DN=DC=AB,
∴NM=EC,
∴ND=MN+DM=EC+DG=AB.
点评 此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识,得出△ADG≌△FDM(ASA)是解题关键.

练习册系列答案
相关题目
19.|a|+a=2a,则a是( )
| A. | 0 | B. | 负数 | C. | 非负数 | D. | 正数 |
20.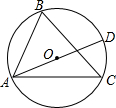 如图,∠BAC=60°,AD为⊙O的直径,AD交BC于E,且BE=2CE,则$\frac{AB}{AD}$的值( )
如图,∠BAC=60°,AD为⊙O的直径,AD交BC于E,且BE=2CE,则$\frac{AB}{AD}$的值( )
 如图,∠BAC=60°,AD为⊙O的直径,AD交BC于E,且BE=2CE,则$\frac{AB}{AD}$的值( )
如图,∠BAC=60°,AD为⊙O的直径,AD交BC于E,且BE=2CE,则$\frac{AB}{AD}$的值( )| A. | 2 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{1}{2}$ |
17.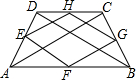 如图,四边形ABCD中,AB∥DC,E,F,G,H分别是各边的中点,分别记四边形ABCD和EFGH的面积为S1和S2,则下列各个判断中正确的是( )
如图,四边形ABCD中,AB∥DC,E,F,G,H分别是各边的中点,分别记四边形ABCD和EFGH的面积为S1和S2,则下列各个判断中正确的是( )
 如图,四边形ABCD中,AB∥DC,E,F,G,H分别是各边的中点,分别记四边形ABCD和EFGH的面积为S1和S2,则下列各个判断中正确的是( )
如图,四边形ABCD中,AB∥DC,E,F,G,H分别是各边的中点,分别记四边形ABCD和EFGH的面积为S1和S2,则下列各个判断中正确的是( )| A. | S1>2S2 | B. | 2S1<S2 | C. | S1=2S2 | D. | $\sqrt{{S}_{1}}$=2$\sqrt{{S}_{2}}$ |
14.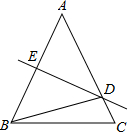 如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于D,交AB于E,∠DBC=15°,则∠A的度数是( )
如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于D,交AB于E,∠DBC=15°,则∠A的度数是( )
 如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于D,交AB于E,∠DBC=15°,则∠A的度数是( )
如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于D,交AB于E,∠DBC=15°,则∠A的度数是( )| A. | 50° | B. | 20° | C. | 30° | D. | 25° |
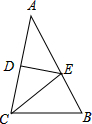 如图,ED为△ABC的AC边的垂直平分线,且AB=5,△BCE的周长为8,则BC的长度为( )
如图,ED为△ABC的AC边的垂直平分线,且AB=5,△BCE的周长为8,则BC的长度为( )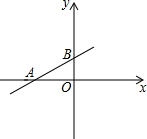 如图,一次函数y=kx+b图象经过点A(-4,0)和点B(0,2).
如图,一次函数y=kx+b图象经过点A(-4,0)和点B(0,2).