题目内容
6. 如图,PA、PB分别与⊙O相切于A、B两点,若∠C=65°,则∠P的度数为50°.
如图,PA、PB分别与⊙O相切于A、B两点,若∠C=65°,则∠P的度数为50°.
分析 先证明∠P=180°-∠AOB,根据∠AOB=2∠ACB求出∠AOB即可解决问题.
解答  解:∵PA、PB是⊙O切线,
解:∵PA、PB是⊙O切线,
∴PA⊥OA,PB⊥OB,
∴∠PAO=∠PBO=90°,
∵∠P+∠PAO+∠AOB+∠PBO=360°,
∴∠P=180°-∠AOB,
∵∠ACB=65°,
∴∠AOB=2∠ACB=130°,
∴∠P=180°-130°=50°,
故答案为50°.
点评 本题考查切线的性质、四边形内角和定理,同弧所对的圆周角与圆心角的关系等知识,解题的关键是切线性质,四边形内角和定理的应用,属于中考常考题型.

练习册系列答案
相关题目
14. 如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )
如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )
 如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )
如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )| A. | ∠ABC=∠DCB | B. | AC=DB | C. | ∠A=∠D | D. | OC=OB |
11.在半径为5cm的⊙O中,圆心O到弦AB的距离为4cm,则弦AB的长为( )
| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
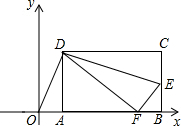 如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(3,4),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点C的坐标为(8,4)或(3$+2\sqrt{5}$,4)或($\frac{43}{6}$,4).
如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(3,4),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点C的坐标为(8,4)或(3$+2\sqrt{5}$,4)或($\frac{43}{6}$,4).
 如图,AB是⊙O的直径,弦AD平分∠BAC,交⊙O于点D,DE⊥AC于点E,求证:DE是⊙O的切线.
如图,AB是⊙O的直径,弦AD平分∠BAC,交⊙O于点D,DE⊥AC于点E,求证:DE是⊙O的切线.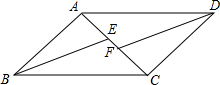 如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F.
如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F.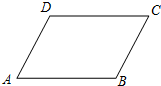 如图,已知四边形ABCD中,AB∥CD,若不添加任何辅助线,请添加一个条件:
如图,已知四边形ABCD中,AB∥CD,若不添加任何辅助线,请添加一个条件: 在?ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
在?ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.